1.3 La aceleración en los móviles que giran

Hemos indicado anteriormente que la velocidad tiene carácter vectorial. Como tal vector podemos distinguir en ella su módulo y la dirección y el sentido. Cuando la velocidad de un objeto varía con el tiempo puede hacerlo bien porque varíe el módulo, porque varíe la dirección y sentido del movimiento o porque varíen ambos aspectos.

Ya sabemos que la magnitud que mide la variación de la velocidad es la aceleración. Es posible definir la aceleración como suma de otras dos:

1. La aceleración tangencial (a_t) que informa del cambio en el módulo de la velocidad.
2. La aceleración normal (a_n) que informa del cambio en la dirección y en el sentido de la velocidad.

En el siguiente cuadro resumimos qué valor tendría cada una de estas dos componentes de la velocidad en los movimientos que hemos estudiado hasta ahora y en el MCU.

Tipo de movimiento	Aceleración tangencial	Aceleración normal	Aceleración
Reposo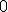
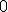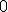MRU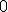
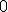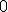MRUA
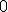MCU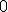

En un MCU, lógicamente la aceleración tangencial es nula porque no varía el ritmo con el que gira el móvil (siempre da las mismas vueltas por segundo). Sin embargo la normal es distinta de cero puesto que la dirección y el sentido cambian constantemente para dibujar la trayectoria circular.

Del mismo modo que en su momento definimos la aceleración lineal como el ritmo del cambio de la velocidad, podemos definir una magnitud que mida el cambio en la velocidad angular.

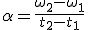
Como la velocidad angular se mide en radianes por segundo, la aceleración angular se mide en radianes por segundo cada segundo, o lo que es lo mismo en radianes por segundo al cuadrado.

En el siguiente apartado veremos que esta aceleración guarda una relación con la aceleración tangencial.

En el caso de un MCU esta aceleración es nula puesto que la velocidad angular se mantiene constante.

Del mismo modo que dedujimos la ecuación velocidad-tiempo para los MRUA, ahora podríamos hacer lo propio con la velocidad angular. Basta despejar de la definición de aceleración angular.

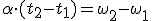
Si consideramos que en el instante inicial nuestro crónometro estaba puesto a cero,

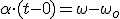
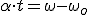
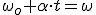
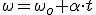
Puedes observar el parecido de esta ecuación con la ecuación velocidad-tiempo de los MRUA. En lugar de velocidades aparecen velocidades angulares y en lugar de la aceleración, la aceleración angular.