6. Lentes delgadas
Fíjate en esta secuencia de imágenes:
 |
 |
 |
 |
 |
|
Imagen de Frank C. Müller en Wikimedia. CC |
Imagen de Arbeiterreserve en Wikimedia. CC0 |
Imagen de Julo en Wikimedia. CC0 |
Imagen de Jgaguilar16 en Wikimedia. CC |
Imagen de Mavavf en Wikimedia. CC |
La serie de objetos son de uso más o menos cotidiano, con un factor común. Todas presentan un sistema óptico formado por lentes.
Una lente es cualquier elemento transparente, homogéneo e isótropo, limitado por dos superficies de la cuales, al menos, una es curva. Su función es hacer que la luz converja o diverja, según interese y, aunque hay lentes de muchos tipos, todas ellas basan su funcionamiento en las leyes de la refracción ya conocidas.
Para poder calcular la desviación de los rayos es preciso realizar una consideración: las lentes han de ser delgadas. Esto significa suponer que las distancias desde el vértice y desde el centro de la lente son las mismas.
En la figura siguiente puedes ver los tipos de lentes más frecuentes y sus representaciones esquemáticas:
 |
 |
| Imagen de Guam modificada por Jfmelero en Wikimedia Commons. CC | Imagen de CharoSaa en Wikimedia Commons. CC |
Como ocurría con los espejos, las lentes forman una imagen de los objetos de los cuales les llega la luz. Podemos conocer dónde se encuentra esa imagen utilizando la llamada ecuación fundamental de las lentes delgadas:
![]()
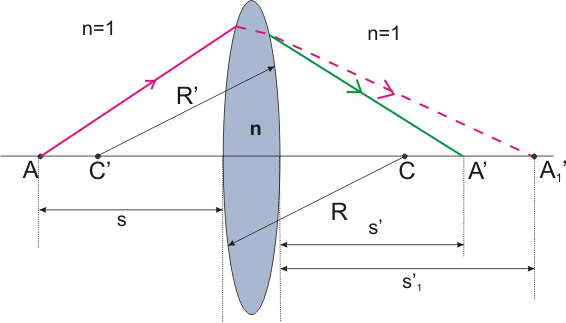
En esta expresión hemos tenido en cuenta que la lente tiene un índice de refracción n y que está situada en el aire. La imagen siguiente te ayudará a comprender mejor esta fórmula.
Por otra parte, de la ecuación fundamental podemos calcular la distancia focal f'. Para ello hacemos s=∞. En ese caso s'=f' y obtenemos la llamada fórmula del constructor de lentes:
![]()
Caso práctico
Deduce la ecuación fundamental de las lentes delgadas a partir de la figura anterior y de la ecuación del dioptrio