3.2. Interpretación de la pendiente
Importante
- m = tg
, siendo el ángulo que forma la recta con la parte positiva del eje OX.
- El cociente entre la segunda y la primera componente de un vector director,
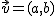, de la recta. Es decir,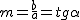 
El valor de la pendiente de una recta coincide con la tangente del ángulo que forma la recta con la parte positiva del eje OX.
En la ecuación explícita de una recta y = mx + n, el valor de m corresponde a la pendiente y n es la ordenada en el origen. Esta ordenada en el origen, indica el valor de la coordenada "y" del punto en que la recta corta al eje OY.
Configura los deslizadores m y n del siguiente applet de Geogebra para reforzar tu conocimiento sobre la pendiente y la ordenada en el origen.
Escena de Luis Miguel Iglesias en geogebra.org.
Comprueba lo aprendido
Reflexiona
Dada la recta r ≡ 5x - 7y + 1 = 0. Averigua:
(1) La pendiente.
(2) La ordenada en el origen.
(3) El punto de corte con el eje OX.
Puedes ayudarte del applet anterior para comprobar tus resultados.
Ejercicio Resuelto
Halla las ecuaciones explícitas correspondientes a los lados: r, s y t del triángulo que se muestra a continuación:
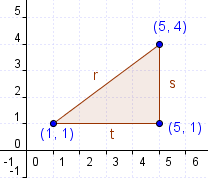
Ejercicio Resuelto
Averigua la ecuación punto-pendiente de la recta que pasa por P = (1,1) y Q = (-4,6)