3.1. Ecuaciones de la recta
La ecuación de una recta es una expresión analítica que permite identificar todos los puntos de la recta y conocer sus coordenadas.
Vamos a determinar la ecuación de una recta, a partir de un punto, 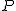 , que pertenezca a ella y de un vector director,
, que pertenezca a ella y de un vector director, 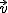 , que esté en la dirección de la recta.
, que esté en la dirección de la recta.
Escena de iedamatematicas en geogebra.org
Comprueba lo aprendido
Retroalimentación
Falso
Horizontal, es referente a la dirección que depende del vector director de la recta, . Por tanto no es posible
. Por tanto no es posible
Retroalimentación
Verdadero
Podemos lograrlo ya que la posición no depende del vector director, .
.
Retroalimentación
Verdadero
Claro que es posible, puesto que para obtener una recta horizontal, basta cambiar , colocando paralelo al eje OX.
, colocando paralelo al eje OX.
Retroalimentación
Verdadero
Claro que es posible. Basta cambiar la dirección de la recta, modificando su vector director, .
.
Usaremos una u otra ecuación para expresar la recta, en función de la información que conozcamos de la misma:
Se pueden presentar distintos casos. Destacamos los siguientes:
Todas los tipos de ecuaciones, así como las transformaciones que nos permiten pasar de una a otra se recogen en la siguiente tabla:
| DISTINTAS MANERAS DE EXPRESAR LA ECUACIÓN DE UNA RECTA. | ||||||||||||||||||
|
Introducción. Por dos puntos del plano pasa una y sólo una recta. Por tanto, una recta queda determinada, o bien, : · Conocidos dos puntos pertenecientes a ella, o, · Conocidos un punto y un vector director de la misma. El vector director es cualquier vector que una dos puntos de dicha recta. _________________________________________________________________________________________________________ Ecuación de una recta. La ecuación de una recta es una expresión que nos permite calcular las coordenadas de cualquiera de sus puntos.
_________________________________________________________________________________________________________ Distintas maneras de expresar la ecuación de una recta. La Ecuación Vectorial es la ecuación desde la que partiremos para obtener el resto de tipos de ecuaciones con las que se puede expresar una recta.
|
||||||||||||||||||
Importante
+ Caso 1. Conocemos un punto y su vector director, que indica la dirección de la misma.
+ Caso 2. Conocemos dos de sus puntos. Con estos puntos podemos formar su vector director y estaríamos en el Caso 1.
* Caso 2.1. Conocemos los dos puntos de corte, tanto con el eje OX como con el eje OY. Da igual qué puntos sean. En definitiva, conocemos dos puntos de ella, es decir, estaríamos en el Caso 2.
+ Caso 3. Conocemos un punto de ella y su pendiente, es decir, la inclinación de la recta con respecto al eje OX.
* Caso 3.1. Conocemos su pendiente y el punto de corte con el eje OY. Al fin y al cabo, conocemos un punto y su pendiente luego, estamos en el Caso 3.
Applet de Geogebra de Luis Miguel Iglesias. Ecuaciones Vectorial y Paramétricas de una recta.
Comprueba lo aprendido
Completa los huecos que faltan en las siguientes afirmaciones:
Caso práctico
Vamos a practicar con distintos casos:
(1) Obtén las ecuaciones paramétricas y continua de la recta r que pasa por P = (1,2) y su vector director es 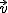 = (1,-1)
= (1,-1)
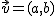 y pasa por un punto
y pasa por un punto 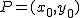 .
.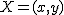 es un punto cualquiera de la recta, este se obtendrá como suma del vector de posición del punto
es un punto cualquiera de la recta, este se obtendrá como suma del vector de posición del punto 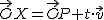 (
(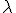 , depende del autor. Aquí se ha optado por la letra t).
, depende del autor. Aquí se ha optado por la letra t). 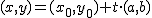
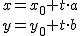
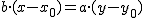
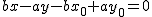
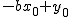 , obtenemos:
, obtenemos: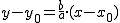
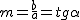 donde α es el ángulo que la recta forma con el eje de abscisas y m la pendiente, inclinación de la recta.
donde α es el ángulo que la recta forma con el eje de abscisas y m la pendiente, inclinación de la recta.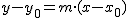
 , y llamando
, y llamando