Desintegración radiactiva
Imagina que tenemos delante una muestra radiactiva. Si pudiéramos fijarnos en un núcleo concreto no tendríamos forma de saber cuándo se va a desintegrar (transformarse en otro por emisión de partículas α o β) porque este proceso, para un núcleo particular, ocurre al azar. Afortunadamente para nosotros, cualquier muestra radiactiva contiene una cantidad enorme de núcleos, y esto nos permite analizar este asunto de forma estadística.
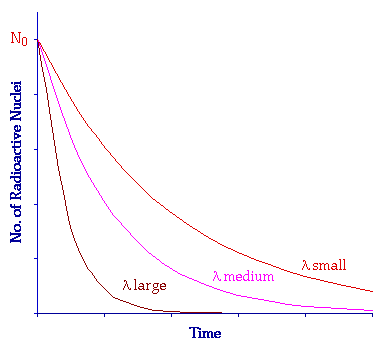
En cualquier caso, la disminución temporal de núcleos de la muestra por desintegración en otros será una función del número de núcleos que haya y de la muestra concreta que estemos observando (no se desintegra a la misma velocidad el C-14 que el U-238, por ejemplo).
|
Imagen en Wikimedia Commons de KieranMaher |
Los matemáticos expresan esta dependencia de la siguiente forma:
donde λ es una magnitud llamada constante de desintegración radiactiva, representa la probabilidad de que un núcleo se desintegre en la unidad de tiempo y es característica de cada núclido. Su unidad en el Sistema Internacional es el Becquerel, definido como desintegración por segundo:
La ecuación anterior se llama ecuación diferencial. No es muy difícil de resolver (es posible que a estas alturas de curso sepas hacerlo), pero a nosotros no nos interesa tanto el procedimiento como la solución, que es la siguiente:
Esta expresión nos permite conocer el número de núcleos (N) que quedan sin desintegrar de una muestra que inicialmente tenía N0 al cabo de un cierto tiempo t. En el apartado siguiente comprobarás la utilidad que tiene la fórmula obtenida.
Como ves, el número de núcleos de la muestra disminuye con el tiempo de forma exponencial. Esta exponencial será más o menos suave en función del valor de λ. La imagen te presenta una gráfica para tres núclidos diferentes.
Se llama período de semidesintegración (T) al tiempo que tarda una muestra radiactiva en reducirse a la mitad por desintegración de la otra mitad.
Podemos obtener una expresión para este tiempo calculando el tiempo que tardan los N0 núcleos en reducirse hasta N0/2
Por otra parte, la fórmula sería útil experimentalmente si pudiéramos ir contando núcleos en cada momento. Hay una manera más fácil si te das cuenta que cada núcleo que se desintegra emite una partícula (α o β), de forma que el número de núcleos que se desintegran es igual al número de partículas emitidas. Y este número es fácil de contar, disponemos de contadores Geiger que detectan las partículas emitidas.
Al número de desintegraciones que se producen por unidad de tiempo se le llama actividad radiactiva (A). En el SI se mide en Bequerel (Bq) y se puede calcular simplemente multiplicando la constante de desintegración por el número de núcleos en cada instante.
Por la forma en la que hemos definido A, es fácil comprender que se cumple:
Como puedes comprobar en los ejercicios resueltos, esta fórmula es muy útil para determinar la edad de muestras muy antiguas.
Finalmente se define la vida media (τ) como el promedio del tiempo que tarda el núcleo de una muestra en desintegrarse. Se cumple lo siguiente:
La siguiente simulación presenta un juego de datación radiactiva.
|
|
| Simulación en phET-Universidad de Colorado bajo licencia Creative Commons |
Caso práctico
1) Un núcleo radiactivo tiene un periodo de semidesintegración de 1 año. ¿Significa esto que se habrá desintegrado completamente en dos años? Razonar la respuesta.
2) La actividad de 14C (T1/2 = 5700 años) de un resto arqueológico es de 120 desintegraciones por segundo. La misma masa de una muestra actual de idéntica composición posee una actividad de 360 desintegraciones por segundo.
a. Explicar a que se debe dicha diferencia y calcular la antigüedad de la muestra arqueológica.
b. ¿Cuántos átomos de 14C tiene la muestra arqueológica en la actualidad? ¿Tienen ambas muestras el mismo número de átomos de carbono?