2.5 Campo magnético creado por una espira conductora
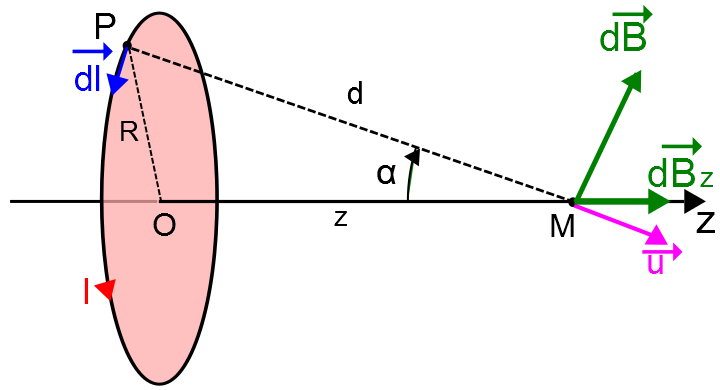
Imagen en WIKIMEDIA COMMONS de Xzapro4 de |
Ya has analizado como se determina el campo magnético creado por un conductor que no es recto y sabes que es necesario aplicar la ley de Biot-Savart para su determinación teórica.
Pues bien, aquí se determinará el campo creado por un conductor que tiene forma circular y es plana al que se conoce por espira. No hace falta que te llame la atención sobre la simetría de la espira. Debido a la misma, las proyecciones del vector campo magnético sobre el plano de la espira se anularán, mira la imagen. Luego quiere decir que el campo magnético creado en el eje de la espira sólo tendrá la dirección de éste.
No quiere meterte en berenjenales, ya tendrás bastante cuando empieces una carrera. Por ello, te suelto de sopetón la solución tras aplicar la integral a ley de Biot-Savart.
![]()
Cuando se pretende calcular el campo magnético creado por la espira en su centro, es decir, cuando, la coordenada "z" es cero. La expresión se reduce a:
![]()
Visita esta animación es bastante ilustrativa
Caso práctico
Se una espira de 4 cm de radio por la que circula una corriente de 10 A. μ0=4π·10-7N·A-2.
¿Cuánto vale el campo creado en en su centro?
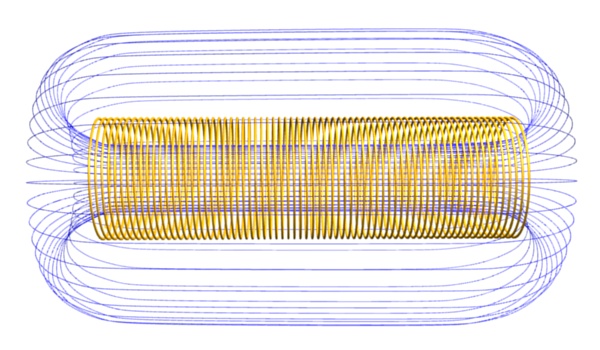
Imagen en WIKIMEDIA COMMONS de Perox de |
Un caso especial es el solenoide, que viene a ser un objeto que resulta por combinación de espiras circulares como la anterior.
Una definición más técnica de un solenoide sería la que sigue: cualquier dispositivo que puede crear en su interior un campo magnético uniforme e intenso y, por el contrario, muy débil en el exterior.
Un ejemplo del mismo sería un hilo conductor enrollado formando espiras circulares, es decir, el hilo tiene una forma helicoidal. Si se le introduce en medio un núcleo o barra de hierro se le llama al sistema bobina.
El campo magnético creado en su interior depende del número de vueltas y la longitud del hilo conductor, piensas que se puede enrollar el hilo de muchas formas, es decir, las vueltas pueden tener un diámetro diferente.
La expresión es muy semejante a la correspondiente a la espira. Multiplicando la misma por el número de espiras y sustituyendo el denominador por la longitud del hilo.
![]()
Como se puede llegar a esa expresión, para que no te agobies, es fácil de entender, ya conoces el resultado del campo magnético creado por un conductor rectilíneo, luego esto se puede generalizar para otras disposiciones.
¿Cómo actuar? Con simple lógica, la idea se fundamenta en dividir en pequeños trozos que puedan considerarse rectilíneos, y posteriormente sumar, perdón, integrar, las participaciones en el campo global como se ha realizado en la espira.
Los más complicado es tener manejo del cálculo integral, cuyas bases esenciales aprenderás en matemáticas que espero que no te resulte tedioso.