2. Intervalos
 . . |
|
Bajo licencia de creative commons |
Eva está esperando el autobús para ir al trabajo, sabe que de 9:05 a 9:10 pasa el autobús nº 6. Hoy el autobús ha llegado a las 9 horas 5 minutos 4 segundos. Pero ayer, como estaba lloviendo, llegó a las 9 horas 8 minutos 3 segundos. Tanto en este ejemplo, como en muchos otros, estamos usando de forma inconsciente intervalos de números reales. En nuestro caso, Eva tiene que esperar un intervalo de 5 a 10 minutos.
Para representar los intervalos se usan paréntesis ( ) y corchetes [ ]. Así, la expresión matemática de este intervalo será [5, 10]. Y si designamos por x la hora de llegada del autobús, lo podemos expresar en forma de desigualdad: 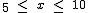 .
.
 |
|
www.todomonografias.com/images/2007/04/104420.gif. Bajo licencia de creative commons |
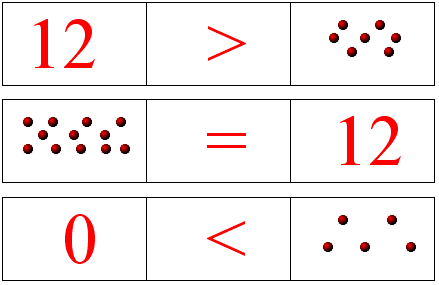
Veamos el significado de estos símbolos:
El símbolo < se lee "menor que".
Así 2 < 5 se lee 2 menor que 5.
Si escribimos x < 5 representamos a todos los números reales "x" que son menores que 5, por ejemplo el 1, el - 1, o el 2,7.
El símbolo > se lee "mayor que".
Así 5 > 2 se lee 5 mayor que 2.
Si escribimos x > 2, estamos representando a todos los números reales que son mayores que 2.
El símbolo 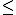 se lee "menor o igual que", así
se lee "menor o igual que", así
x 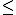 2 representa a todos los números reales que son menores o iguales que 2.
2 representa a todos los números reales que son menores o iguales que 2.
El símbolo 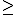 se lee "mayor o igual que", así
se lee "mayor o igual que", así
x 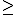 2 representa a todos los números reales que son mayores o iguales a 2.
2 representa a todos los números reales que son mayores o iguales a 2.
Los símbolos, 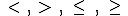 se pueden leer en los dos sentidos, es decir,
se pueden leer en los dos sentidos, es decir, 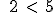 se puede leer : "dos menor que 5", o "5 mayor que 2".
se puede leer : "dos menor que 5", o "5 mayor que 2".
La expresión![]() , indica todos los números, "
, indica todos los números, "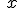 ", que son mayores que 2 y menores o iguales que 5.
", que son mayores que 2 y menores o iguales que 5.
Actividad
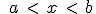 . Son todos los números reales comprendidos entre a y b sin incluir ni a ni b.
. Son todos los números reales comprendidos entre a y b sin incluir ni a ni b.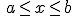 . Son todos los números reales comprendidos entre a y b ambos incluidos.
. Son todos los números reales comprendidos entre a y b ambos incluidos.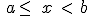 . Son todos los números reales comprendidos entre a y b in incluido a pero no b.
. Son todos los números reales comprendidos entre a y b in incluido a pero no b.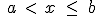 . Son todos los números reales comprendidos entre a y b incluido b pero no a.
. Son todos los números reales comprendidos entre a y b incluido b pero no a.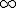 , a) =
, a) = 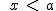 . Son todos los números reales menores que a.
. Son todos los números reales menores que a.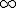 , a] =
, a] = 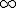 ) =
) = 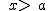 . Son todos los números reales mayores que a.
. Son todos los números reales mayores que a.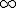 ) =
) = 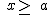 . Son todos los números reales mayores o iguales que a.
. Son todos los números reales mayores o iguales que a.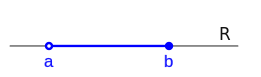 es la representación gráfica del intervalo (a,b]
es la representación gráfica del intervalo (a,b]Pre-conocimiento
 |
|
Bajo licencia de creative commons |
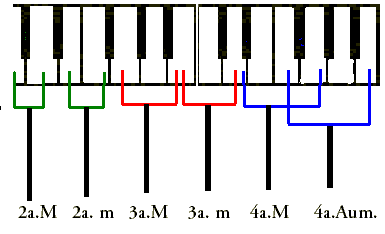
¿Sabías que en música también se utilizan los intervalos?
Pues sí, en música, la distancia entre dos sonidos se conoce como intervalo musical.
Caso de estudio
|
|
|
|
Escribe en forma de desigualdad los siguientes intervalos y semirrectas:
a) (-2, 3)
b) [-2, 3)
c) [-2, 3]
d) (-2, 3]
e) [-1, +![]() )
)
f) (-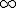 , 5)
, 5)
Pregunta Verdadero-Falso
 |
|
bajo licencia de creative commons |
Retroalimentación
Falso
La solución es:Retroalimentación
Verdadero
La solución es [2, 5)Retroalimentación
Verdadero
La solución es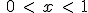
Retroalimentación
Falso
La solución es (-7, -3]Retroalimentación
Verdadero
La solución es (-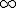 , 0)
, 0)
Retroalimentación
Falso
La solución es