1.1. La recta real
De momento tenemos un montón de números por ahí sueltos. Veamos, tenemos los naturales, los enteros, los racionales - dependiendo del tipo de decimales, recuerda que hay tres tipos-, y por último, los irracionales; y como ya sabes, todos juntos hacen los números reales.
Pero eso, todos sueltos por ahí. Deberíamos buscar un sitio donde tuviésemos a todos ordenados y así si queremos echar mano de uno saber donde está, y encontrarlo fácilmente.
Bien, pues ese sitio donde tenemos a todos los números reales (naturales, enteros, racionales e irracionales) se llama recta real.
Actividad
La recta real
Os presento a la recta real.
 |
| fuente propia realizado con GeoGebra |
Solo hemos representado a los números enteros, pero ahí dentro están todos, vamos a centrarnos en cualquier parte de la recta real y veamos que hay dentro. Por ejemplo, vamos a hacer un zoom entre los números 1 y 2, y después haremos un zoom entre 1,4 y 1,5; y posteriormente entre 1,41 y 1,2; y así sucesivamente, podríamos seguir infinitamente.
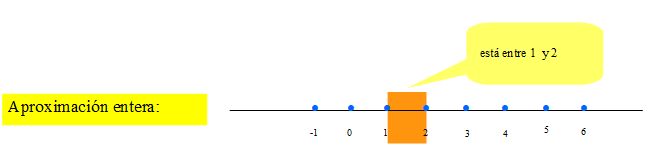 |
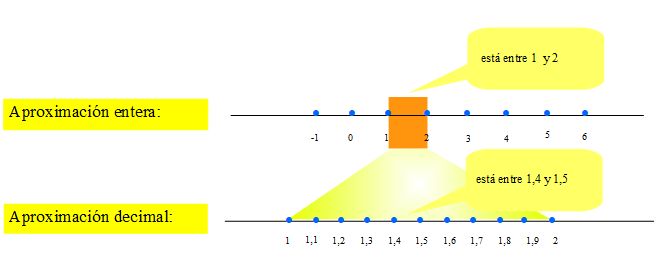 |
 |
| fuente propia |
Igualmente que hemos situado a los decimales, podemos situar a las fracciones o bien a los números racionales.
Y cómo no, podemos situar a los números irracionales, eso si, esta vez nos cuesta mucho trabajo.
Hay un método para representar cada tipo de número, pero eso forma parte de otra historia, vamos a ver un ejemplo de representación de número irracional de forma aproximada.
 |
| fuente propia |
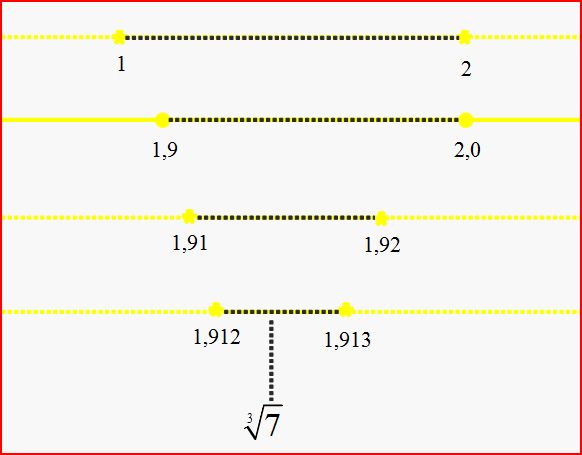
En la imagen de arriba vamos aproximando poco a poco el valor de raíz de 7. Si aproximamos a la unidad, podemos situar su valor entre 1 y 2. Si lo aproximamos a la décima, situamos su valor entre 1,9 y 2. Si seguimos aproximando a la centésima, su valor estará entre 1,91 y 1,92. Un paso más es aproximar a la milésima, o sea, el valor estará entre 1,912 y 1,913. Este proceso, es infinito, nunca llegaríamos a obtener el resultado exacto de la raíz de 7, tan solo, una aproximación, ya que al ser un número irracional, tiene infinitos decimales.
Caso de estudio
En el siguiente applet (pizarra interactiva, en la cual puedes manipular algunas cosas) puedes cambiar los números, situándolos donde tú creas que están.