2.3. Tipificación
|
| Imagen en Flickr de HckySo bajo CC |
¿Y qué hacemos para calcular probabilidades del resto de distribuciones Normales, es decir con media distinta de cero y desviación típica distinta de 1? ¿Hay tablas para todas?
No, por suerte solo hay una tabla de la distribución Normal, la de la estándar. Por lo que para conocer probabilidades de otras Normales tenemos que recurrir a herramientas tecnológicas como las hojas de cálculo o aprender a tipificar.
¿Tipificar? Sí, vamos a realizar un cambio de variable de cualquier Normal a la estándar que no va a modificar la probabilidad. A continuación, hallaremos la probabilidad de la estándar, y por tanto la de la Normal inicial.
¿Un cambio de variable que mantiene la probabilidad? Ese hecho no es tan extraño. ¿Recuerdas que la probabilidad de que una Normal estuviera en el intervalo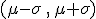 
era 0.683 y este valor no dependía del valor de la media ni de la desviación típica? Pues lo mismo ocurre con otro tipos de intervalos.
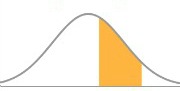
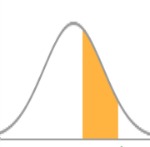
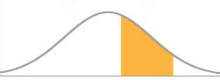
En las siguientes imágenes aparecen tres Normales diferentes, cada una con su media y desviación típica. Pero las probabilidades de las tres áreas coinciden porque las veces que se han sumado las desviaciones típicas a las medias son iguales en los tres casos:
 |
 |
 |
| Imágenes de elaboración propia |
||
Importante
- Si a una variable aleatoria le restamos un número, la media
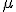de la variable disminuye también en ese número. - Del mismo modo, si la dividimos por un número, la desviación típica
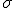de la variable también queda dividida por ese número.
Una consecuencia de las dos propiedades anteriores es la siguiente:
Si queremos transformar una variable Normal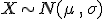 
, en otra variable Z Normal estándar 
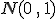, le restamos 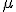a 
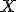y luego la dividimos entre .
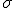Es decir, si 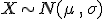, entonces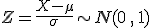 
A este proceso, que mantiene las probabilidades, le llamaremos tipificar una variable aleatoria continua.
Como ejemplo, vamos a calcular la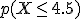 
sabiendo que 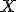es una 
.
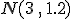En primer lugar, si hacemos el cambio indicado arriba, tenemos que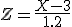 
es una 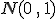. Vamos a operar:
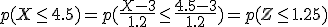
Las tablas de la Normal estándar nos dicen que la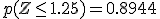 
, y por tanto 
.
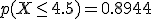A continuación puedes ver un vídeo del canal de juanmemol donde se resuelve un problema en contexto usando la tipificación de una distribución Normal:
Ejemplo o ejercicio resuelto
|
| Imagen en Flickr de Diego López bajo CC |
El precio del kilogramo de gambas frescas en el mercado de abastos de Huelva sigue una distribución Normal de media 16.5 euros y desviación típica 2 euros.
Responde a las siguientes cuestiones:
a) ¿Cuál es la probabilidad de que un kilogramo de gambas nos cueste menos de 15 euros?
Caso de estudio
 |
Curso 2009/2010
En un colegio se estudia la distribución de la nota de Matemáticas de sus estudiantes, resultando ser una Normal de media 7.2 y desviación típica 1.2. Se elige al azar un estudiante de ese colegio, ¿cuál será la probabilidad de que su nota en esta asignatura sea mayor que 7.5?
Caso de estudio
|
|
Curso 2010/2011
El peso de las manzanas que se producen en una huerta sigue una ley Normal con una media de 150 gramos y desviación típica de 20 gramos.
a) ¿Qué porcentaje de estas manzanas tendrá un peso inferior a 115 gramos?
b) Halla la probabilidad de que una manzana, elegida al azar en este huerto, tenga un peso que se encuentre entre 165 y 220 gramos?
Caso de estudio
|
|
Curso 2011/2012
La duración de un tipo de pilas alcalinas sigue una distribución Normal de media 55 horas y una desviación típica de 6 horas.
a) Calcula la probabilidad de que una pila elegida al azar dure más de 53 horas.
b) Halla la probabilidad de que una pila elegida al azar dure entre 56 y 58 horas.
Ya hemos mencionado anteriormente que una distribución Binomial con un número de repeticiones del experimento grande, tiende a hacerse continua. Incluso vimos al inicio del tema, que en ese caso, los diagramas de barras de las probabilidades se van aproximando a la campana de Gauss.
En general, una binomial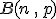 
se parece a una Normal cuanto mayor es el producto 
(o 
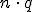si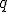 
es mayor que 
).
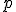De hecho si y 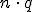son ambos mayores que 3, la aproximación es buena, y si superan 5, es perfecta.
En ese caso la Binomial se transforma en una Normal de media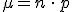 
y desviación típica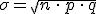 
En el siguiente vídeo se explica este proceso con más detalle: