1.1. Definición
En octubre de 2012 el Instituto Nacional de Estadística (INE) publicaba una encuesta sobre la estructura salarial entre los trabajadores del estado español. De los datos recogidos se extraía el siguiente gráfico. En el eje horizontal se representa el sueldo anual y en el vertical el número de asalariados.
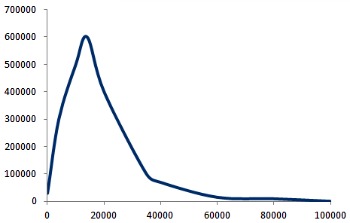
Imagen de elaboración propia |
Podemos considerar la variable aleatoria continua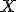 
que a cada sueldo mensual le asocia el número de asalariados que tienen ese sueldo. La gráfica anterior sería la función de probabilidad de .
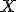En las distribuciones continuas tiene sentido preguntarse por la probabilidad de un intervalo de la variable, pero no un valor puntual de ella.
Por ejemplo, por el estudio del INE sabemos que el salario mediano es de 19.000 euros, por tanto podemos afirmar que 
, ya que el valor mediano divide a una distribución justamente por la mitad.
Dicho de otro modo, el área que hay bajo la gráfica de la función desde el salario 0 y hasta el salario 19.000 euros es igual que el área que hay bajo la curva desde 19.000 y hasta 100.000 euros, por tanto también se tiene que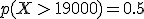 
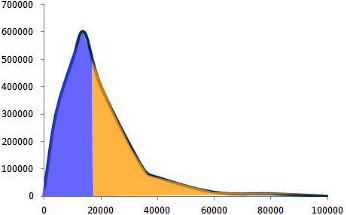
Imagen de elaboración propia |
Importante
Una variable aleatoria continua 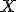queda determinada por una función 
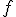que llamaremos función de probabilidad o función de densidad.
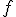debe ser siempre mayor o igual que cero y el área debajo de su gráfica tiene que ser 1.
La probabilidad estará definida como el área delimitada por la gráfica de 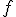y el eje horizontal.
En el caso de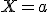 
, dicha probabilidad es cero, 
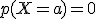, ya que no se encierra ningún área.
Para un intervalo, la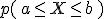 
será igual al área que hay bajo la gráfica de f en el intervalo 
.
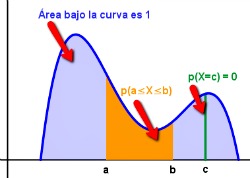
Imagen de elaboración propia |
Como acabamos de ver la 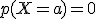, si 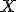es una variable aleatoria continua. Por tanto, el hecho de que los extremos de un intervalo estén o no incluidos en la probabilidad que hay que calcular, no afecta su valor.
Es decir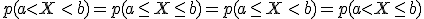 
, ya que la probabilidad de que 
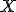sea igual a 
o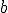 
es cero.
Caso de estudio
Una línea de autobuses pasa cada 20 minutos. Consideramos la variable aleatoria X que determina el tiempo que hay que esperar, en función del tiempo que hace que pasó el autobús la última vez.
La gráfica de su función de densidad sería:
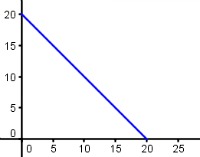
Imagen de elaboración propia |
Determina las siguientes probabilidades:
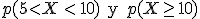
Lo que se nos pregunta es la probabilidad de tener que esperar entre 5 y 10 minutos, y la de tener que esperar al menos 10 minutos.
La media,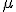 
, y la desviación típica, 
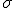, indican los mismos parámetros que en las distribuciones estadísticas. La media indica el centro de gravedad de la distribución y la desviación típica la medida de dispersión.
AV - Pregunta Verdadero-Falso
Responde verdadero o falso a las siguientes cuestiones que se te plantean.
Si 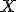es una variable aleatoria continua, entonces:
Retroalimentación
Falso
En una variable aleatoria continua, la probabilidad de un valor concreto siempre vale 0, sea cual sea ese valor.
Retroalimentación
Falso
La función de probabilidad nunca puede ser negativa.
Retroalimentación
Verdadero
Es una de las dos características principales que cumple la función de densidad. Es así, porque la probabilidad máxima o total de cualquier variable vale 1.
Retroalimentación
Verdadero
No hay más que recordar que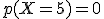 
.
Retroalimentación
Falso
La segunda característica fundamental de la función de densidad es que es una función positiva, es decir, está siempre sobre o por encima del eje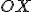 
.