2.3. Cociente y potencias de números complejos en forma binómica
El producto de un número complejo z por su conjugado 
siempre es un número real, es decir:
Además, se observa que 
. Este último resultado nos va a servir para definir el cociente de dos números complejos.
Importante
Dado los números complejos z1 y z2, se define su cociente como el número complejo
En el siguiente applet de Geogebra de Ana Guadalupe Del Castillo puedes practicar el cociente de números complejos. Mueve los puntos z1 y z2 para variar los números complejos.
Ejercicio Resuelto
Dados 
halla 
.
Antes de ver cómo se calculan las potencias de un número complejo hemos de estudiar las sucesivas potencias de i.
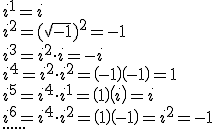
Se observa que las sucesivas potencias de i se repiten después de cuatro pasos, proporcionando tan sólo cuatro valores distintos, i, -1, -i y 1. Como 
, se tiene que 
, cualquiera que sea el número natural k. Para calcular 
bastará expresar el exponente como 4k + r, siendo k un número entero no negativo y el resto r = 0, 1, 2 ó 3. Por tanto,
Y este número será i, -1, -i ó 1, según r valga 0, 1, 2 ó 3.
Ejercicio Resuelto
Halla las siguientes potencias de i.
Importante
Sea z = a + bi un número complejo. Para calcular 
, siendo n un número natural, emplearemos la fórmula del binomio de Newton.
En el siguiente applet de Geogebra de Ana Guadalupe Del Castillo puedes practicar la potencia de un número complejo.
Ejercicio Resuelto
Calcular 
.
Curiosidad
Existen otras dos formas de expresar un número complejo: forma trigonométrica y forma polar, las cuales veremos en el último bloque de este curso ya que se precisan algunos conocimientos de geometría plana.
Dada la complejidad que presenta el cálculo de la raíz de un número complejo en forma binómica, esta operación también se verá más adelante. Para su cálculo es necesario aplicar el Teorema de Moivre, y usar la forma trigonométrica de un número complejo.