2.2. Suma y producto de números complejos en forma binómica
Con los números complejos podemos realizar las operaciones aritméticas básicas (igual que con cualquier otro tipo de número).
Importante
Dados dos números complejos z = a + bi, w = c + di, definimos su suma (z + w) como el nuevo número complejo (a + c) + (b + d)i.
Ejemplo
Si tenemos los números complejos z = 4 + 3i y w = 2 - i, su suma será z + w = (4 + 2) + (3 - 1)i = 6 + 2i.
La suma de números complejos cumple las siguientes propiedades:
- Asociativa
- Existencia de elemento neutro: Existe un número complejo 0 = 0 + 0i tal que, para todo número complejo z, se tiene que z + 0 = 0 + z = z.
- Existencia de elemento opuesto: Para cada número complejo z existe otro número complejo, -z, tal que:
z + (-z) = (-z) + z = 0
- Conmutativa: Dados dos números complejos z y w se cumple:
z + w = w + z
En el siguiente applet de Geogebra puedes practicar la suma de números complejos. Mueve los puntos z1 y z2 para variar los números complejos.
Veamos un ejemplo de operaciones con números complejos:
Vídeo de lasmatematicas.es alojado en Youtube
Importante
El producto del número real λ por el número complejo z = a + bi es el número complejo 
, es decir.
Ejemplo
Dado z = 2 - 3i hallar 4z.
Importante
Dados dos números complejos z = a + bi y w = c + di, el producto como el nuevo número complejo ac - bd + (ad + bc)i. Se realiza de la siguiente forma (teniendo en cuenta que 
):
Ejemplo
Dados z = 2 - 3i y w = 3 + 3i hallar 
.
El producto de dos números complejos cumple las siguientes propiedades.
- Asociativa
- Conmutativa
- Existencia de elemento neutro: Existe el número complejo 1 = 1 + 0i tal que, para todo número complejo z, se tiene que
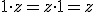. - Existencia de elemento simétrico (inverso): Para todo número complejo
existe otro número complejo,
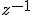, tal que 
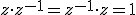. - Distributiva respecto de la suma
En el siguiente applet de Geogebra de Ana Guadalupe Del Castillo puedes practicar el producto de números complejos. Mueve los puntos z1 y z2 para variar los números complejos.
Ejercicio Resuelto
Realiza las siguientes operaciones:
- (3 - 2i) · (4 + 3i)
- (-2 + 4i) · 2i
- (3 + 4i) · (3 - 4i)