4. Estudio de los satélites
 |
La Luna gira alrededor de la Tierra, y el satélite Meteosat también, solo que a una distancia mucho menor.
¿Cuál es el origen de la fuerza centrípeta responsable de esos movimientos de rotación?: la fuerza de atracción gravitatoria entre esos cuerpos. Es decir, su propio peso es la fuerza que hace cambiar continuamente la dirección del vector velocidad, originando en los casos anteriores el movimiento circular uniforme.
Para resolver situaciones en las que intervengan satélites, solamente tienes que tener en cuenta la ley de gravitación universal y los conceptos relacionados con el movimiento circular uniforme, que ya has visto en la unidad anterior.
Actividad
La atracción gravitatoria es el origen de la fuerza centrípeta que permite que los satélites giren alrededor de los planetas.
 |
| Animación de Talifero en Wikimedia Commons. CC0 |
Un satélite es un cuerpo que orbita (está girando) alrededor de otro, siguiendo una órbita elíptica, casi circular.
Podemos hacer una clasificación de los tipos de satélites: pueden ser naturales (cuerpos celestes) o artificiales como los satélites de comunicaciones o meteorológicos.
Pero ¿qué necesita un cuerpo para orbitar? pues debe cumplir con la llamada condición de orbitación: la fuerza gravitatoria es la única fuerza que actúa sobre el satélite y al tratarse de una fuerza normal a la trayectoria provoca solo aceleración centrípeta o normal, es decir el satélite orbita describiendo un movimiento circular uniforme.
Para saber más
¿Por qué los satélites no caen?
 |
| Imagen de Brian Brondel en Wikimedia Commons. CC |
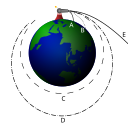
Acabas de leer que los satélites orbitan porque sienten la fuerza de atracción de la gravedad del cuerpo sobre el que orbitan. Entonces ¿por qué no acaban estrellándose sobre la superficie de este?
Se puede explicar utilizando el ejemplo conocido como cañón de Newton, representado en la imagen. Supongamos que un cañón dispara con un cierto ángulo, la trayectoria seguida por la bala es una parábola representada por la letra A, la bala cae a cierta distancia del cañón. Si aumentamos el ángulo de tiro tendríamos la trayectoria B, de forma que la bala llega más lejos del cañón, pero sigue cayendo al suelo. Si aumentásemos mucho el ángulo podría darse la situación representada por la letra C, la bala nunca llega a tocar el suelo debido a la curvatura de la Tierra, quedando así en órbita.
A continuación veremos cómo determinar la velocidad orbital, el período de revolución de un planeta o satélite e incluso la velocidad a la que has de lanzar un objeto para que llegue al infinito.