Resumen
Importante
La expresión general de un sistema de dos ecuaciones lineales con dos incógnitas es el siguiente:
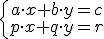 donde a, b, c, p, q y r son números y las variables son x e y.
donde a, b, c, p, q y r son números y las variables son x e y.
Un ejemplo cualquiera podría ser 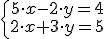
La solución de un sistema de ecuaciones está formada por aquellos valores que al sustituirlos en las incógnitas verifican todas y cada una de la ecuaciones del sistema.
Por ejemplo, en el sistema 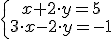 serían solución los valores x = 1 e y = 2 ya que se cumplirían las dos ecuaciones.
serían solución los valores x = 1 e y = 2 ya que se cumplirían las dos ecuaciones.
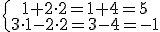
Importante
Atendiendo al número de soluciones del sistema, podemos realizar la siguiente clasificación:
- Sistema compatible determinado. Tiene una sola solución.
- Sistema compatible indeterminado. Tiene infinitas soluciones.
- Sistema incompatible. No tiene solución.
Importante
Llamaremos ecuaciones equivalentes a aquellas que, siendo distintas, tienen las mismas soluciones. Este concepto se amplía a los sistemas de ecuaciones: dos sistemas serán equivalentes si tienen las mismas soluciones.
- Si la ecuación ax + by = c se multiplica o divide por un número distinto de cero, la ecuación resultante es equivalente a la anterior.
Por ejemplo la ecuación 10x + 5y = 25 es equivalente a la ecuación 2x + y = 5 que se ha obtenido dividiendo todos los coeficientes entre 5.
- Si en un sistema a una ecuación se le suma o resta otra ecuación distinta, la ecuación obtenida es equivalente a la primera.Es decir, si tenemos las ecuaciones
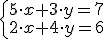 , la ecuación que se obtiene restando a la de arriba la de abajo,
, la ecuación que se obtiene restando a la de arriba la de abajo,  , es equivalente a ambas.
, es equivalente a ambas.
Importante
El método de reducción para resolver sistema de ecuaciones se compone de los siguientes pasos:
- Se multiplican una ecuación, o las dos, por números convenientes (que debes elegir tú) para que nos queden dos ecuaciones en las que una de las incógnitas vaya multiplicada por el mismo número cambiado de signo.
- Se suman las dos ecuaciones término a término (ya sabes, los términos semejantes entre sí).
- Tras el paso anterior nos queda una ecuación con una sola incógnita. La resuelves como hiciste en el tema 2.
- El valor de la incógnita resuelta se sustituye en cualquiera de las dos ecuaciones primeras y nos queda una ecuación con una sola incógnita, la que aún no sabemos. Se resuelve y ya tienes la solución completa del sistema.
Importante
Un sistema de ecuaciones se resuelve por el método de sustitución a través de los siguientes pasos.
- En una de las ecuaciones se despeja una de las incógnitas en función de la otra.
- La incógnita despejada se sustituye en la otra ecuación, con lo que obtenemos una ecuación donde solo hay una incógnita.
- Se resuelve la ecuación obtenida obteniendo el valor de una de las variables.
- Se sustituye el valor obtenido en la variable despejada en el apartado 1 y se obtiene la otra incógnita.
Importante
Los pasos a seguir en el método de igualación son los siguientes:
- Despejamos en las dos ecuaciones la misma incógnita.
- Igualamos entre sí los dos valores despejados. De esa manera obtenemos una ecuación donde sólo aparece la otra incógnita.
- Se resuelve la ecuación obtenida. Así tenemos el valor de una de las incógnitas.
- Se sustituye el valor de la incógnita encontrada en cualquiera de las dos expresiones despejadas en el paso 1 y se halla el valor de la otra incógnita.
Importante
Un sistema de ecuaciones de segundo grado es aquel en el que aparece al menos una ecuación de grado 2. Los sistemas de ecuaciones de segundo grado son de tipo no lineal, y para su resolución aplicaremos los métodos utilizados en los sistemas de primer grado, aunque normalmente se emplea el método de sustitución.