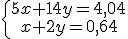5. Resolución de problemas

Imagen de George Pólya en Wkipedia. Licencia CC

Lo más importante para enfrentarnos a cualquier situación o problema en la vida cotidiana es una buena planificación. A continuación, vamos a describir algunas reglas para que podamos usar estrategias adecuadas en la resolución de problemas matemáticos.

La resolución de problemas es uno de los motores de la matemática, y por tanto de su enseñanza. Podemos afirmar sin temor a equivocarnos que aprender matemáticas es aprender a resolver problemas.

El matemático y pedagogo húngaro George Pólya (1887-1985) fue, a mediados del siglo pasado, el personaje clave a la hora de destacar la importancia de la resolución de problemas en la enseñanza, tanto de la matemática como de otras disciplinas. Polya considera la resolución de problemas como uno de los ejes esenciales de la educación matemática.

Importante

Pólya resumió en los siguientes pasos la mejor estrategia para resolver problemas:

Entender el problema: es fundamental que leamos el enunciado del problema detenidamente para entender bien, tanto lo que en él se describe como la pregunta que se nos plantea. ¿De qué datos disponemos? ¿Cómo podemos relacionarlos? ¿Qué matemáticas podemos aplicar? ¿Hemos resuelto algún problema similar anteriormente?
Configurar un plan: debemos buscar las variables adecuadas, relacionarlas entre ellas y así como con los datos conocidos. A continuación, plantearemos la ecuación o ecuaciones.
Ejecutar el plan: resolvemos la ecuación o el sistema planteado utilizando el método más adecuado.
Mirar hacia atrás: comprobamos que la solución obtenida es correcta, conforme al enunciado y a la situación del problema planteado. Revisamos todo el proceso.

Caso práctico

Vamos a seguir los cuatro puntos anteriores para resolver el siguiente problema.

"Juan quiere hacer publicidad de su tienda de ropa en la prensa local. Por ello, está interesado en insertar un anuncio en los periódicos gratuitos que se reparten por las calles. Ha preguntado a dos dueños de locales cercanos al suyo, y le han informado de que el precio depende del número de palabras que aparezcan en él y del tamaño en centímetros cuadrados que tenga el anuncio.

A la papelería cercana a su local, por un anuncio de 40 palabras y 10 centímetros cuadrados le han cobrado 130 euros. En tanto que el farmacéutico ha pagado 120 euros por un anuncio de 30 palabras y 12 centímetros cuadrados".

Ayuda a Juan a saber cuál es el precio de cada palabra y del centímetro cuadrado del anuncio.

Retroalimentación

Sigamos los pasos de Pólya para resolver el problema.

Entender el problema	Nos preguntan por el precio de cada palabra y del centímetro cuadrado, si quiero insertar un anuncio en la prensa. Conocemos lo que le han cobrado a dos comerciantes.
Configurar un plan	Llamamos x = precio en euros por cada palabra, e y = precio en euros por cada centímetro cuadrado. Con estas dos incógnitas y según los datos que disponemos, planteamos el siguiente sistema:
Ejecutar el plan	Resolvemos por el método más adecuado el sistema. Si dividimos la primera ecuación entre 10 y la segunda entre 6, nos queda el sistema equivalente: Despejamos la y en la primera ecuación y= 13-4x, y la sustituimos en la segunda ecuación, 5x+2(13-4x)=20. Resolvemos la ecuación: 5x-26-8x = 20. Por tanto x = 2, e y = 5.
Mirar hacia atrás.	Comprobamos si las soluciones se ajustan a la pregunta planteada en el problema. Para ello vemos que si el coste de cada palabra es 2 euros, y el de cada centímetro cuadrado 5, se cumplen los precios pagados por los comercios vecinos. Es decir:

Reflexiona

Móvil

Imagen de Jan Vasek en Pixabay. Licencia CC

Vamos a resolver paso a paso un problema que se le ha planteado a Juan con la factura de su teléfono móvil.

Últimamente Juan está observando que gasta mucho en el teléfono móvil, por lo que desea saber cuánto le cuestan el establecimiento de llamada y el minuto de conversación. Al mirar en internet el consumo semanal, resulta que la semana pasada le facturaron 40,4 euros por 50 llamadas que tuvieron una duración de 140 minutos. La anterior, le cobraron 38,4 euros por 60 llamadas y 120 minutos de conversación.

¿Puedes ayudarle?

En esta primera autoevaluación vamos a dar el primer paso: entender el problema, ver los datos de que disponemos y saber qué se nos pregunta.

Comprueba lo aprendido

Pregunta

Ahora es el momento de que diseñemos un plan. Necesitamos saber: cuáles son las incógnitas, cómo las llamamos, qué ecuación o sistema de ecuaciones se nos plantea.

Entre las siguientes opciones debes elegir la única que corresponde al planteamiento del problema. Fijate bien en las incógnitas propuestas en cada apartado pues de ello depende que el sistema tenga sentido o no.

Respuestas

Opción 1

a) x = el número de llamadas, y = el precio del establecimiento de llamada. El sistema queda: .

Opción 2

b) x = el precio del establecimiento de llamada, y = el coste de cada minuto hablado. Quedando el sistema: .

Opción 3

c) x = cantidad de minutos hablados, y = precio de cada minuto hablado. El sistema es: .

Opción 4

d) x = coste del minuto hablado, y = el precio del establecimiento de llamada. Nos queda el sistema: .

Retroalimentación

No sólo es cuestión de elegir bien las incógnitas, sino de plantear las ecuaciones en función de ellas.

Has visto que los cuatro sistemas eran iguales, y pero para que la expresión fuera la solución correcta, debía elgirse como primera incógnita el establecimiento de llamada y como segunda el precio de cada minuto hablado.

Comprueba lo aprendido

Tercer paso, nos toca llevar adelante nuestro plan. En este caso, resolver el sistema

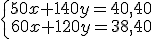
por el método que nos resulte más cómodo.

Reflexiona

Nos queda el último paso: mirar hacia atrás. ¿Qué acciones debemos realizar para quedarnos tranquilos de que hemos resuelto correctamente el problema?

En el siguiente vídeo puedes ver más problemas resueltos. Antes de ver las soluciones de los problemas, para el vídeo e intenta resolverlos.

Vídeo de Tuto Mate alojado en YouTube.

Comprueba lo aprendido

En el siguiente enlace tienes algunas actividades interactivas para practicar los pasos en la resolución de problemas. Utilízalas para repasar y preparar la tarea. Tienes un total de 10 actividades para practicar.

Enlace a las actividades

Curiosidad

Antes de terminar tu aventura por la resolución de problemas, nunca viene mal una sonrisa. En el siguiente vídeo verás cómo se enfrenta a un problema de matemáticas un alumnado muy especial.

Vídeo El Chavo y las matemáticas alojado en YouTube.