Resumen

Una variable aleatoria es continua si al realizar el experimento aleatorio, entre cada dos valores, el número de valores que puede tomar es infinito.

Por ejemplo, la altura de una persona, la longitud del dedo índice, el peso de un perro, el caudal de un río...

Si X es una variable aleatoria continua, la probabilidad de que tome un valor concreto es cero.

 P[X = a] = 0, para cualquier valor de a.

En una variable aleatoria continua, las probabilidades que calculamos están siempre asociadas a intervalos.
Si X es una variable aleatoria continua, la probabilidad de que X esté en un intervalo es el área del recinto limitado por el intervalo y la función de densidad (o función de probabilidad).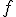
debe ser siempre mayor o igual que cero y el área debajo de su gráfica tiene que ser 1.
En el caso de tener una variable aleatoria continua X, ya hemos visto que las probabilidades de valores concretos son 0. Así, al describir un intervalo, no influye que la desigualdad sea estricta o no para calcular la probabilidad.

P (X ≤ a) = P (X < a)

P (a< X < b) = P (a ≤ X < b) = P (a < X ≤ b) = P (a ≤ X ≤ b)

Imagen de elaboración propia

Se define la función de distribución, F(x), como: F(x)= P [X≤ x]

Una variable aleatoria continua X sigue una distribución normal de media μ y desviación típica σ, y se representa X ~ N(μ,σ) si se cumple que su función de densidad viene dada por:

La gráfica de esta función es similar a esta:

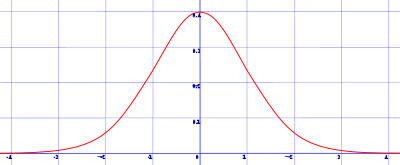
Debido a la forma que adopta se le llama campana de Gauss

La función de densidad de una variable aleatoria Normal es la curva Normal o campana de Gauss. Su gráfica es una función continua, simétrica, cuyo máximo coincide con la media de la distribución.

Para cada valor de la media y cada valor de la desviación típica, existe una curva Normal y su distribución asociada que llamaremos .

Para transformar una variable aleatoria normal en Normal N(0,1), primero se le resta la media de la variable, y el resultado se divide entre la desviación típica:

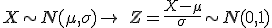
A este proceso se le llama tipificar la variable.

Cálculo de probabilidades en una distribución Normal.

Si "a" es un número positivo y Z sigue una distribución N(0,1):

• P(Z < a) → A partir de la tabla de probabilidades de una distribución N(0,1)
• P(Z > a) = 1 - P( Z < a)
• P(Z < -a) = 1 - P( Z < a)
• P(Z > -a) = P ( Z < a )
• P(a < Z < b) = P(Z < b) - P(Z < a)

Si X es una variable aleatoria discreta que sigue un modelo binomial de parámetros n y p ( X→ B(n , p) ), X se puede aproximar a un modelo normal de parámetro n·p y 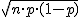si se cumplen las condiciones para "n" y "p":

• n ≥ 30
• n·p ≥ 5 y n·(1-p) ≥ 5

Si se cumple esto, la variable quedaría aproximada por este modelo normal:

A este resultado se le conoce como Teorema de De-Moivre