5. Aproximación de la distribución binomial por la normal
¿Te acuerdas de la binomial? Sí, el tema anterior. El modelo en el que se repetía una serie de veces un experimento, había solamente dos posibles resultados, éxito y fracaso, y contábamos el número de éxitos.
Por ejemplo, si lanzabas 8 veces una moneda y contabas el número de caras, eso era una binomial con n = 8 y p, probabilidad de éxito en un lanzamiento igual a 0,5;
X= n.º de caras → B(8; 0,5)
Si sigue recordando, la fórmula para calcular la probabilidad de un valor en este modelo era: 
¿Te imaginas que repetimos la prueba 50 veces y queremos calcular la probabilidad de que al menos obtengamos 20 caras? Al menos 20 significa 20 o más, o sea, que tendríamos que calcular la probabilidad de X=20, de X=21, de X=22,..., y así hasta X=50. ¡Casi nada!
Pues bien, cuando hacemos que el tamaño de la muestra o de las repeticiones sea suficientemente grande, el modelo binomial se puede aproximar al normal, pero claro, ¿a qué normal? Pues al que tiene como media la media de esa distribución binomial y como desviación típica la desviación típica del modelo binomial. Y entonces todos esos cálculos se van a facilitar.
Pero otra cuestión que hay que tener en cuenta es el valor del parámetro "p". Repite lo anterior con "p" muy pequeño ( menor que 0,1) y después con "p" muy próximo a 1 (entre 0,9 y 1). Ya no se parece tanto, ¿verdad?
Luego tenemos que fijar un criterio para considerar que la aproximación es buena, y ese criterio es que "n" tiene que ser suficientemente grande, y por ello entendemos al menos 30 y que "p" no sea ni muy grande ni muy chico, y para eso, hemos de comprobar que n·p sea por lo menos 5 y n·(1-p) también.
Importante
Si X es una variable aleatoria discreta que sigue un modelo binomial de parámetros n y p ( X→ B(n , p) ), X se puede aproximar a un modelo normal de parámetro n·p y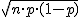 
si se cumplen las condiciones para "n" y "p":
- n ≥ 30
- n·p ≥ 5 y n·(1-p) ≥ 5
Si se cumple esto, la variable quedaría aproximada por este modelo normal:
A este resultado se le conoce como Teorema de De-Moivre
Caso práctico
¿Recuerdas a Jorge?, pues el próximo puente lo va a pasar de turismo en Sevilla y de camino probará suerte en el Gran Casino Aljarafe, aunque lo de Jorge más que probar es ganar casi seguro.
Con suficiente antelación hizo su reserva de hotel para los tres días que iba a pasar en la capital de andaluza.
Los hoteleros son conscientes de que mucha gente reserva plaza por si acaso, pero que después cuando llegue el momento no van a hacer uso de ella y le van a dejar colgada la habitación. Manejan la cifra de que aproximadamente el 15% de las personas que reservan una plaza, luego no aparecen.
Pues bien, en el hotel donde Jorge reservó la habitación se han aceptado 104 reservas para ese fin de semana, pese a que el hotel sólo dispone de 97 habitaciones. ¿Qué probabilidad hay de que Jorge se quede sin habitación y tenga que buscar otro hotel?
Comprueba lo aprendido
Solución
Para saber más
Corrección por continuidad
Como ya sabes, la distribución binomial es discreta, y por tanto, tiene sentido calcular probabilidades puntuales (P[X=a]), mientras que en la normal, al ser continua esto carece de sentido.
La aproximación de una variable discreta X por una continua a la que llamaremos X', genera un cierto error que se corrige modificando el intervalo cuya probabilidad se quiere calcular. Estas son situaciones y correcciones posibles:
- P(X=a) = P( a -0,5 ≤ X' ≤ a + 0,5)
- P(X ≤ a) = P( X' ≤ a + 0,5)
- P(X < a) = P( X' ≤ a - 0,5)
- P(X > a) = P( X' ≥ a + 0,5)
- P(X ≥ a) = P( X' ≥ a - 0,5)
A esta corrección se le conoce como corrección de Yates, debido a que su autor fue el matemático inglés Frank Yates (1902-1994)