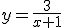2. Todas las funciones de proporcionalidad inversa
Todas las funciones de proporcionalidad inversa tienen esa forma aunque esas rectas a las que la función se acerca sin llegar a tocarlas pueden ser diferentes de los ejes coordenados, como sucedía en el apartado anterior.
Aquí tienes unos ejemplos:
 |
 |
 |
 |
Pero ¿cómo saber si nos dan una ecuación que es una función de proporcionalidad inversa? porque siempre tiene alguna de estas formas:
Claro que los números pueden ser diferentes, o de distinto signo, pero la "forma" de la ecuación sería la misma. Fíjate que lo común en los tres casos es que todas tienen un denominador con una "x"
AV - Actividad de Espacios en Blanco
Vamos a comprobar si distingues los diferentes tipos de funciones que hemos trabajado. Rellena los espacios con la letra que corresponda según la siguiente leyenda:
- A = función afín
- L = función lineal
- C = función constante
- P = parábola
- I = proporcionalidad inversa
- N = ninguna
Representar estas funciones es nuestro próximo objetivo. Para eso lo más importante es encontrar esas rectas a las que la función se acerca y que tienes marcadas en verde en esta gráfica. Esto es lo que te vamos a explicar en el apartado siguiente.
Y una vez que las tengas, el resto es sencillo: