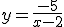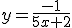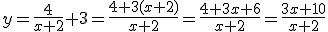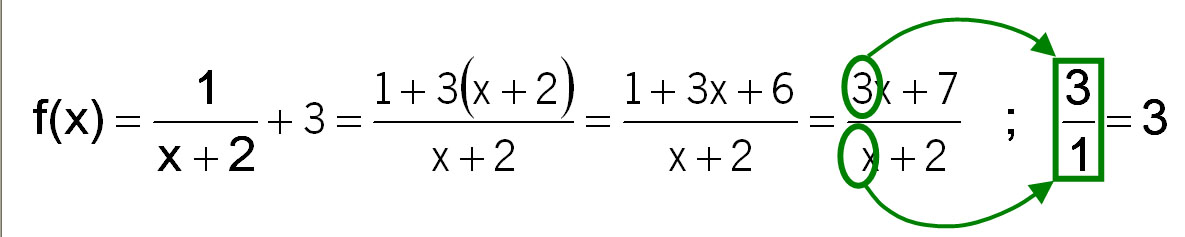2.1 Calcular asíntotas

Una vez que localicemos estas asíntotas, el resto es facilísimo, así que vamos a ver la forma de encontrarlas con un ejemplo. Vamos a hacerlo con la siguiente función:

 

 

 

Cálculo de la asíntota vertical

1. Igualamos el denominador a 0:

x-3 = 0

2. Despejamos x:

x = 3

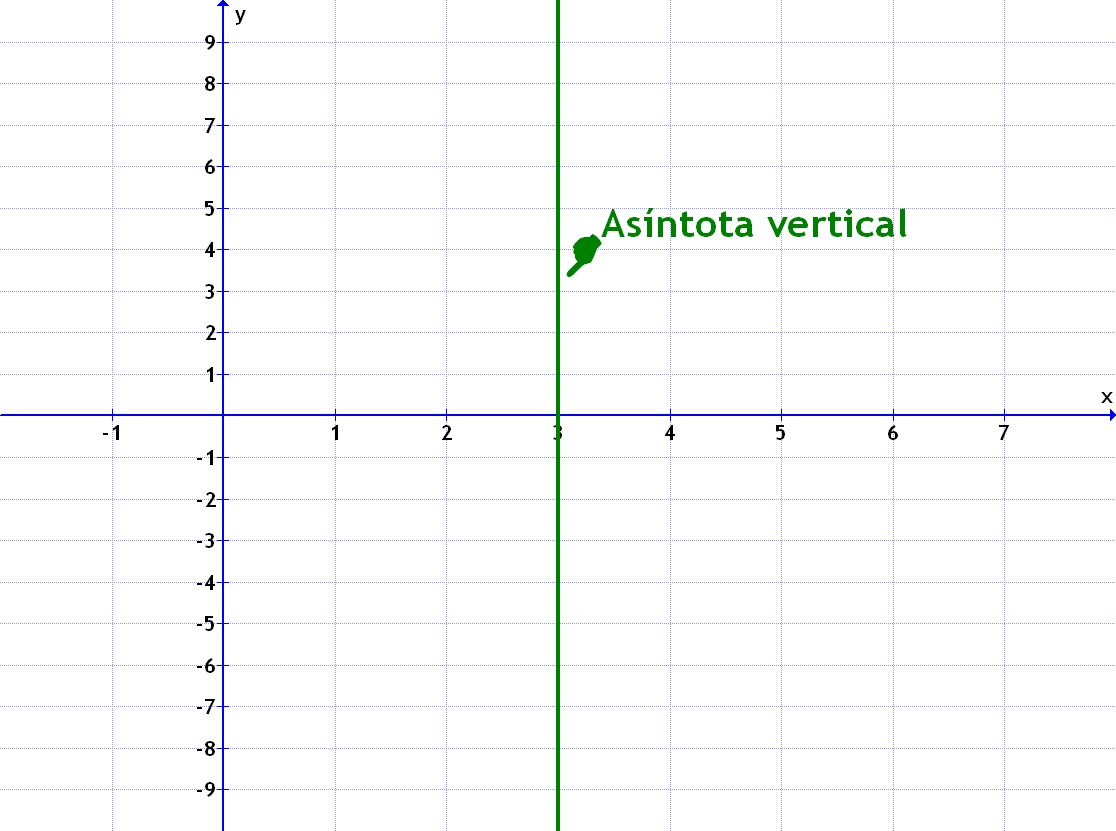
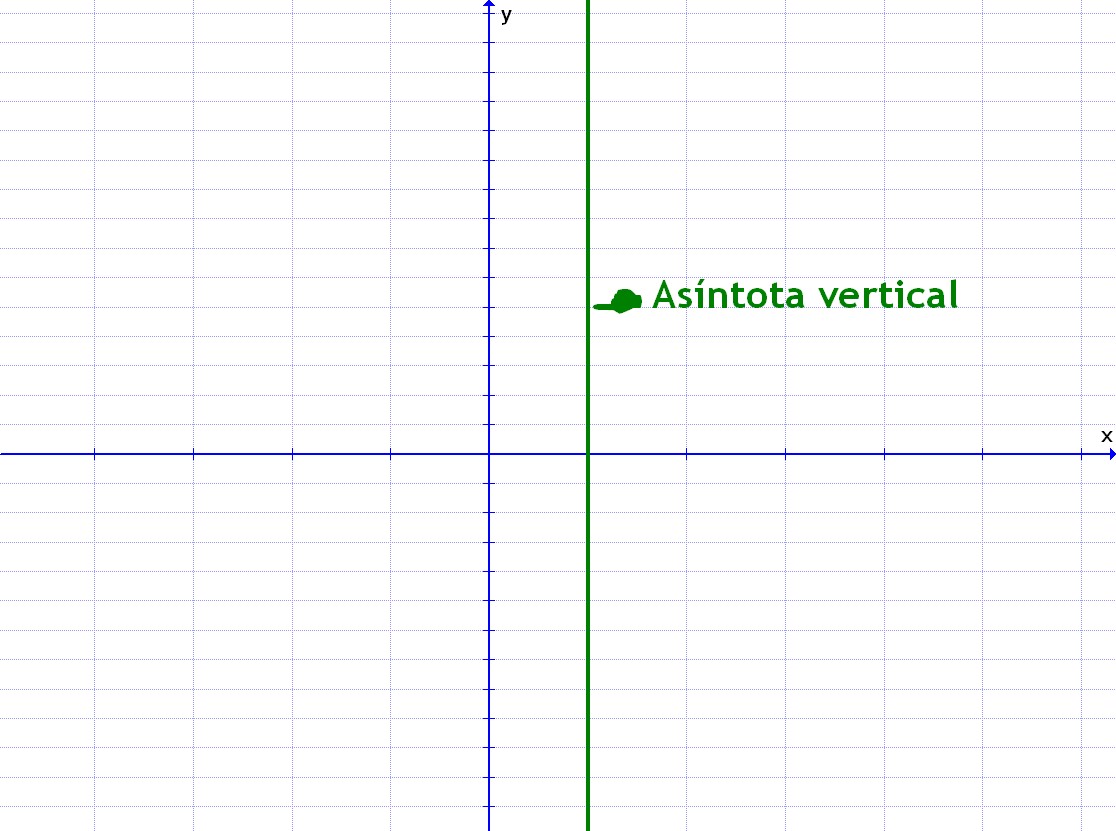
3. Ese número indica la asíntota vertical:


Pulsar sobre la imagen para ampliar

¿fácil, no?

AV - Reflexión

Representa en unos ejes las asíntotas verticales de las siguientes funciones de proporcionalidad inversa:

1. 

 

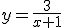
2.

 

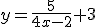
3.

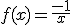
Cálculo de la asíntota horizontal
Esta vez la forma de calcularlo depende del tipo de ecuación que tengas. Vamos a verlo, por lo tanto, tipo a tipo:
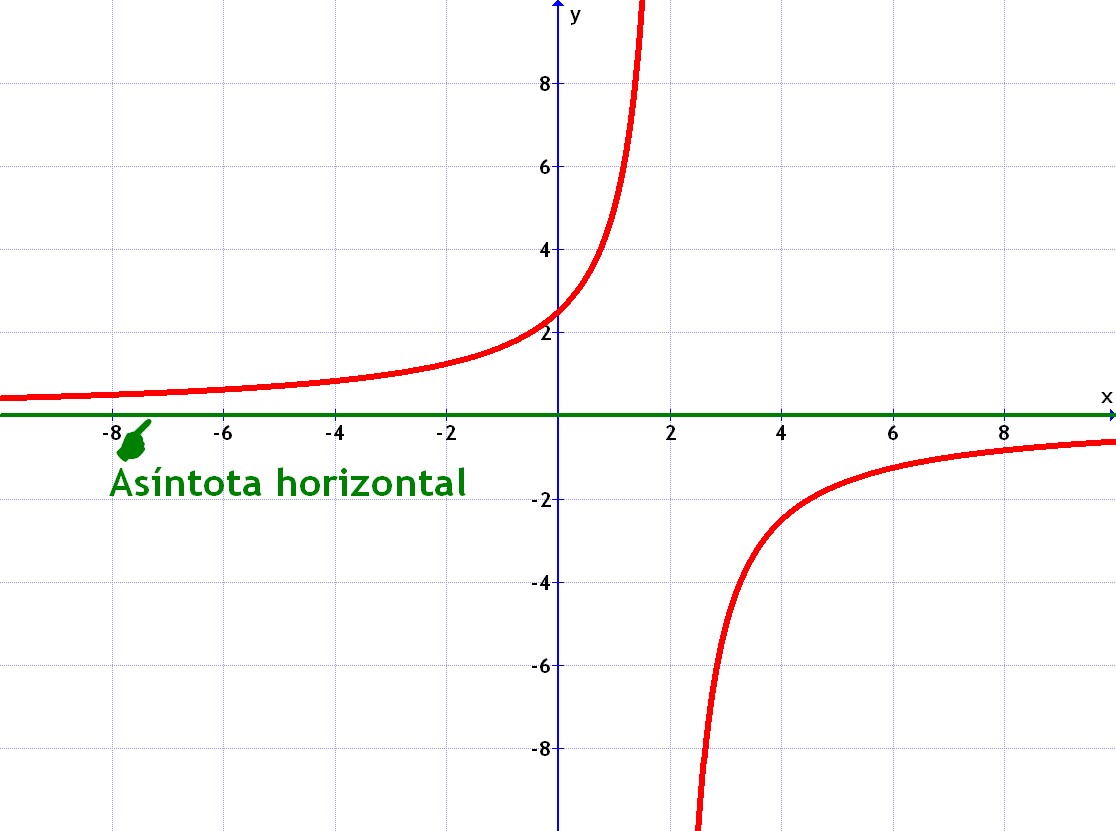
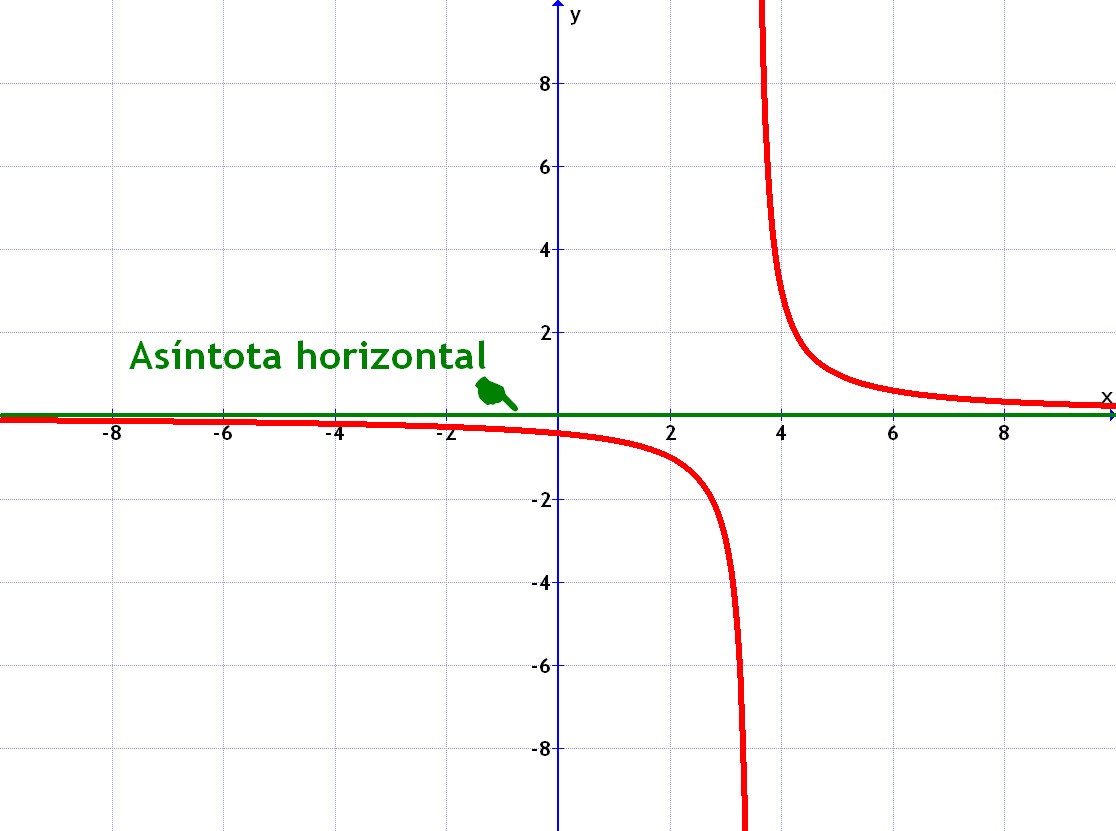
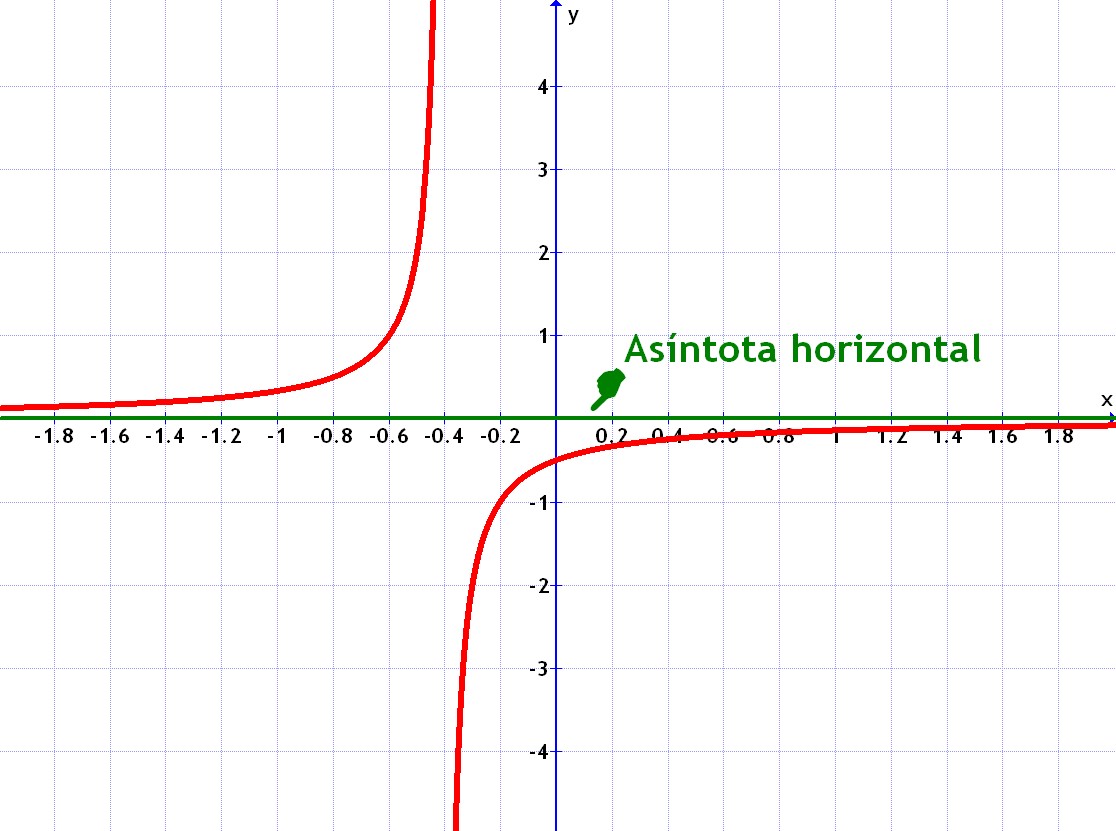
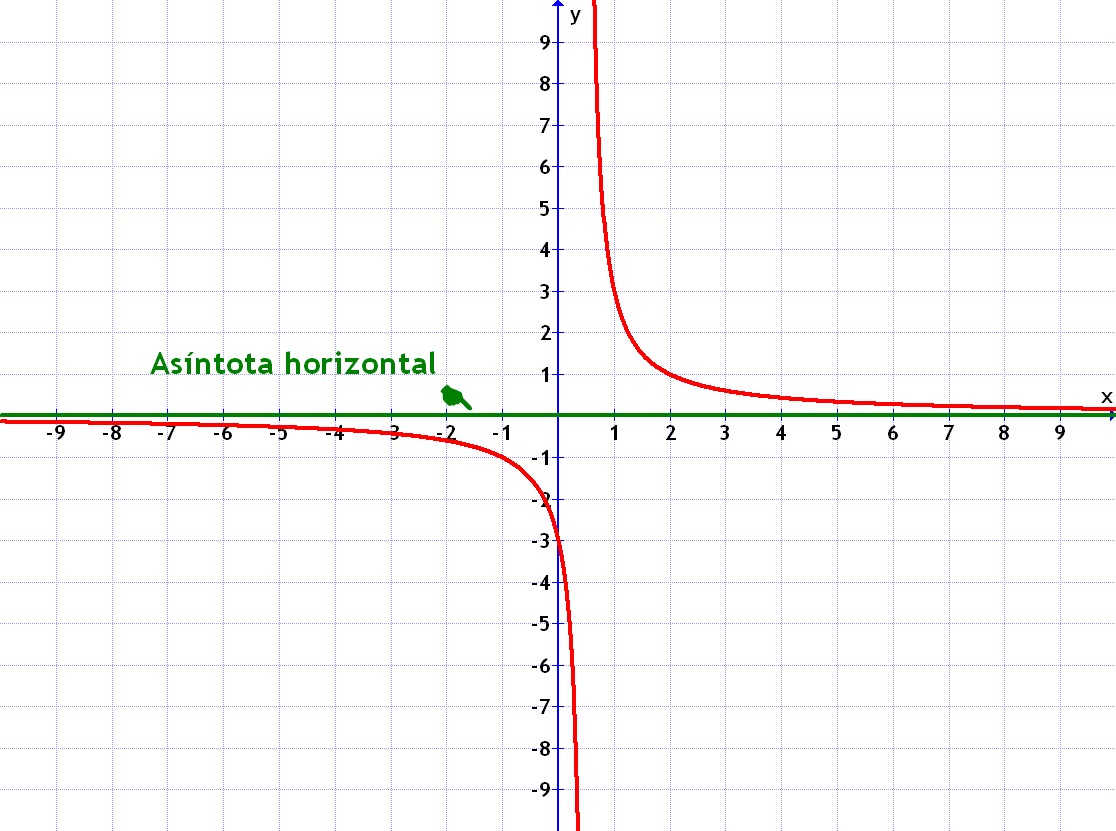
  • Si es del tipo fracción con "x" abajo y número arriba, entonces la asíntota horizontal es el eje de las "x".
Por ejemplo todos estos casos tienen esa asíntota horizontal:
Pulsar sobre las imágenes para ampliar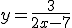

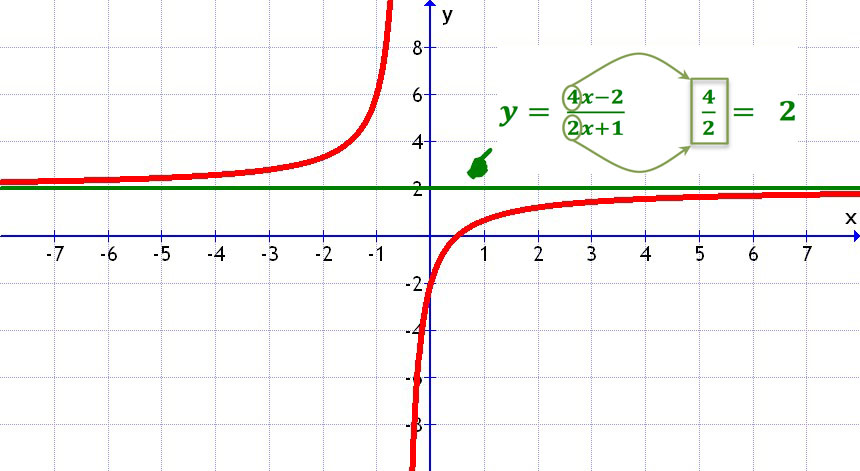
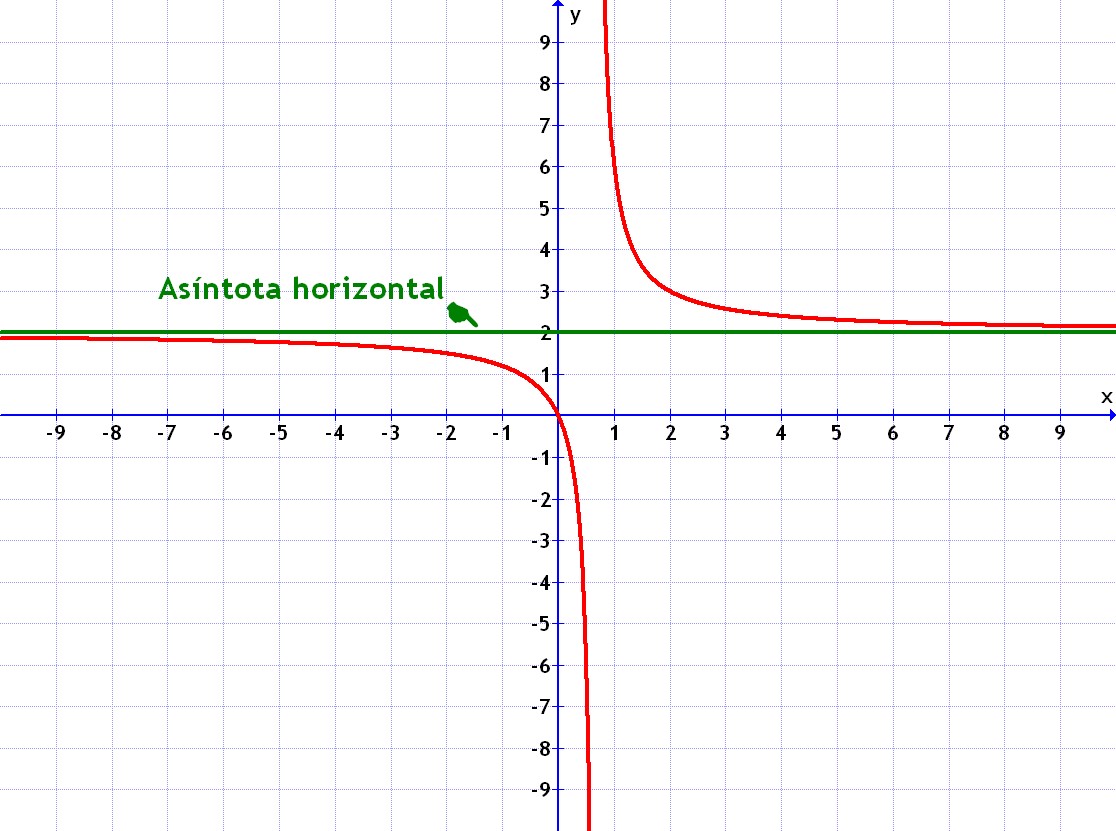
  • Si es del tipo fracción con "x" arriba y "x" abajo como en:
En este caso el sitio en el que está la asíntota horizontal viene determinado por los coeficientes de la "x" de esta forma:
Pulsar sobre la imagen para ampliar

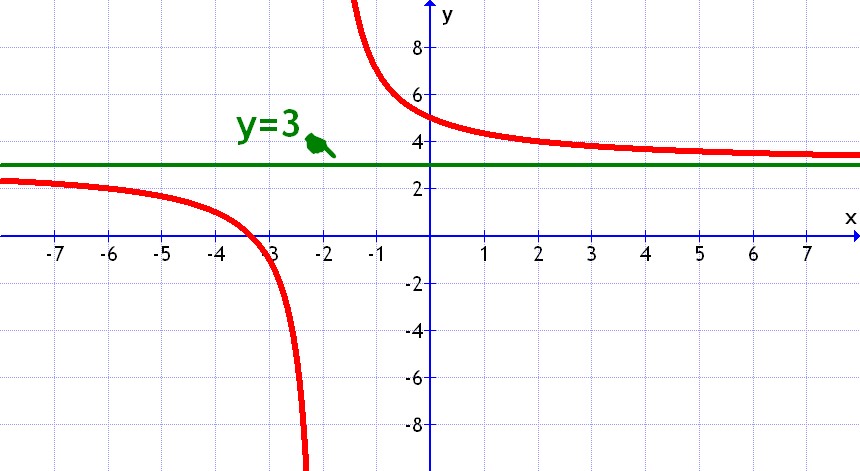
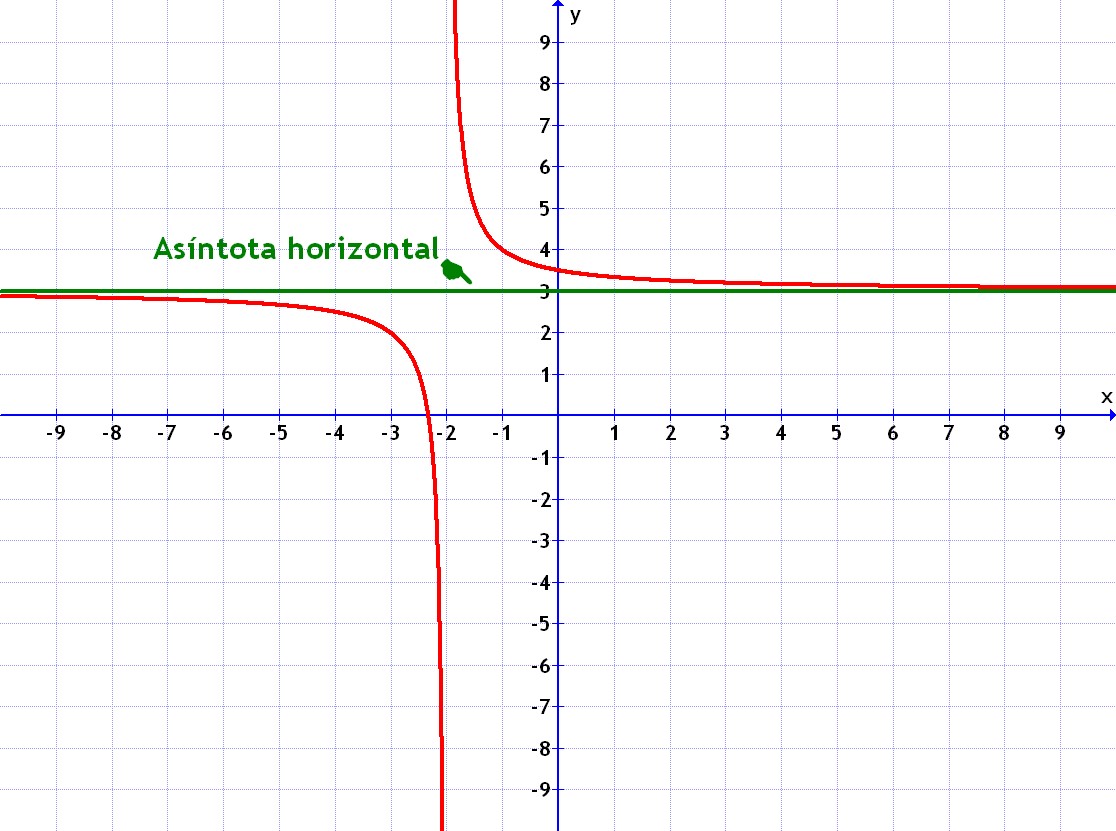
  • Si es del tipo de una fracción más un número, como en el caso 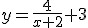hay que hacer esa operación para que nos quede como en el caso de antes:
en este caso la asítota vendría indicada por , es decir 3

Pulsar sobre la imagen para ampliar

AV - Reflexión

Dibuja la asíntota horizontal en estas funciones de proporcionalidad inversa:

1.     
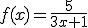
2.    
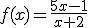
3.   

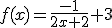
Actividad

Una función de proporcionalidad inversa tiene una recta horizontal y otra vertical a las que la función se acerca que se sitúan siguiendo estas instrucciones:

 

  • Asíntota vertical: se iguala el denominador a cero y se despeja. El nº que sale indica dónde está:

Pulsa sobre la imagen para ampliar

  • Asíntota horizontal: 
    • Es el eje de las x si la función es del tipo:   
Pulsa sobre la imagen para ampliar

 

  • Es la fracción formada por los números que acompañan a las "x" en el caso de fracciones con "x" arriba y abajo. Ejemplo:

→

 

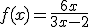Pulsa sobre la imagen para ampliar


  • Es como el caso anterior si la función es una fracción más número. Ejemplo: 
      →

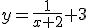
Pulsa sobre la imagen para ampliar