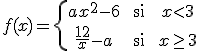3. Función continua en un punto
Sabemos que, conocida la gráfica de un función, podremos afirmar si es continua o no si podemos dibujarla sin levantar el lápiz del papel. Ahora nos toca prestar nuestra atención a por qué "tenemos que levantar el lápiz del papel", en el caso de que exista discontinuidad. Es decir, ¿por qué una función es continua o discontinua en un punto?
Para este estudio no será necesario fijarnos en las funciones lineales, cuadráticas y polinómicas en general, ya que son continuas. Tampoco tendremos que mirar las funciones exponenciales, logarítmicas, senos y cosenos, pues también lo son.
La mayoría de las funciones que no son continuas se encuentran entre las funciones de proporcionalidad inversa, racionales, tangentes y definidas a trozos.
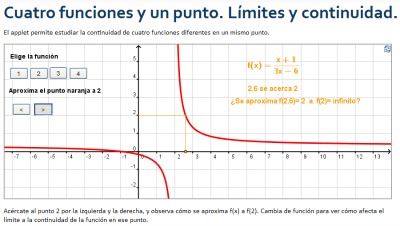
Si haces clic en la siguiente imagen, podrás acceder a una escena de GeoGebra en la que es posible estudiar la continuidad de cuatro funciones diferentes en el punto  . La escena dispone de seis botones, cuatro sirven para seleccionar las distintas funciones, y los otros dos para mover un punto que se aproxima a 2. Mira con detenimiento qué ocurre con
. La escena dispone de seis botones, cuatro sirven para seleccionar las distintas funciones, y los otros dos para mover un punto que se aproxima a 2. Mira con detenimiento qué ocurre con  cuando
cuando 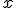 se acerca a 2. De ese modo podrás deducir qué diferencias existen en esa aproximación teniendo en cuenta que la función sea o no continua en
se acerca a 2. De ese modo podrás deducir qué diferencias existen en esa aproximación teniendo en cuenta que la función sea o no continua en 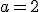 .
.
Podemos afirmar que una función no es continua en un punto por tres motivos: que no esté definida la función en dicho punto, que no exista el límite de  cuando
cuando 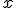 tiende al punto, o que aún existiendo el límite y la función en el punto, ambos valores no coincidan.
tiende al punto, o que aún existiendo el límite y la función en el punto, ambos valores no coincidan.
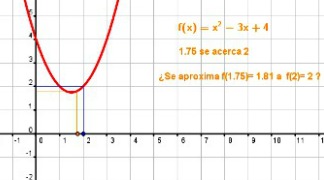 |
Para la función cuadrática,  es continua en 2. Se cumplen los tres requisitos: es continua en 2. Se cumplen los tres requisitos:Existe 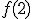 , también existe , también existe 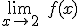 , y ambos valores coinciden. , y ambos valores coinciden. |
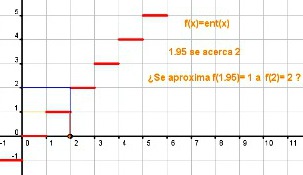 |
Para la función a trozos,  no es continua en 2: no es continua en 2:Existe 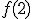 , pero no existe , pero no existe 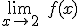 , ya que los límites laterales son diferentes. , ya que los límites laterales son diferentes.Por la izquierda tiende a 1 y por la derecha a 2. |
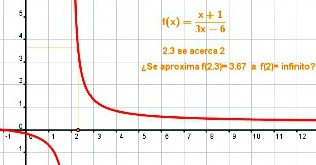 |
Para la función de proporcionalidad inversa,  no es continua en 2. no es continua en 2.No existe ni 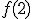 , y además , y además 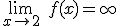 . . |
Actividad de rellenar huecos
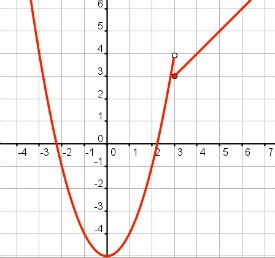
Vamos a estudiar la continuidad de la función que aparece representada en la imagen.

Imagen de elaboración propia
Para ello completa las siguientes frases:
Actividad
Una función  se dice continua en un punto
se dice continua en un punto 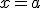 , si
, si  se aproxima a
se aproxima a 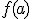 cuando
cuando 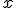 se acerca a
se acerca a  , o lo que es lo mismo, si cumple las siguientes tres condiciones:
, o lo que es lo mismo, si cumple las siguientes tres condiciones:
- Que exista
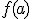
- Que exista
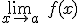
- Que los dos valores anteriores coincidan, es decir,
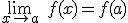
En caso contrario, la función se dirá discontinua en dicho punto.
Una función que es continua en todos los puntos donde está definida, se dirá continua.
En el siguiente enlace puedes ver una clasificación de los distintos tipos de discontinuidades y su relación con la existencia o no del límite en un punto, o de los límites laterales.
Clasificación de discontinuidades
Actividad de rellenar huecos
Para estudiar la continuidad de esta función definida por partes, es conveniente que completes los huecos que aparecen en las siguientes afirmaciones.
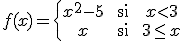
Caso de estudio
 para que la siguiente función sea continua.
para que la siguiente función sea continua.
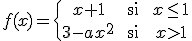
Caso de estudio
 |
Curso 2010/2011
Halla el valor de la constante  para que la función
para que la función
sea continua en todos los números reales.