2.2. Límites laterales
 |
| Imagen de elaboración propia |
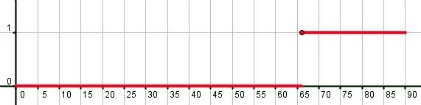
¿Recuerdas el partido entre el Gijón y el Osasuna? ¿Sí, aquel que terminó con un 1-0, siendo Barral, jugador del Spórting, quien marcó el único tanto del encuentro en el minuto 66?
De aquel partido, la función que nos interesaba era la que asociaba a cada instante del partido los goles que se habían marcado hasta ese momento. Su gráfica era la que aparece en la imagen de la derecha.
En la definición de límite en un punto a, centrábamos nuestra atención en cómo varía 
cuando 
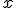se acerca a 
. Pero al punto nos podemos acercar por la izquierda o por la derecha. Es decir, para valores menores que o mayores que 
.
En el partido, nos podemos acercar a 66 por instantes anteriores o posteriores. Para instantes anteriores,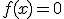 
puesto que aún no se ha marcado el gol. En tanto que para instantes posteriores 
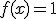ya que se ha marcado el gol.
Eso quiere decir que no tiene límite cuando 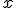tiende a 66. Lo que, como ya habíamos visto, implicaba que no era continua en 66. En este caso, jugar en el "green" del 66 da lugar a un buen salto.
Actividad
Si se acerca a 
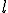cuando 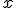se aproxima al punto para valores menores que , diremos que 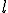es el límite por la izquierda de en el punto .
Y se expresa: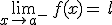 
.
Si se acerca a 
cuando 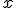se aproxima al punto para valores mayores que , diremos que es el límite por la derecha de en el punto .
Se escribe: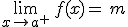 
.
Si los dos límites anteriores coinciden, existe el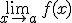 
y es igual a ese valor común.
En la función del partido de fútbol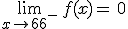 
y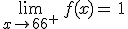 
. Por tanto, como ambos valores no coinciden, se tiene que 
.
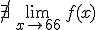AV - Reflexión
Las tarifas postales del servicio de Correos para envío de paquetes, durante el año 2011 vienen expresadas en la siguiente tabla:
 |
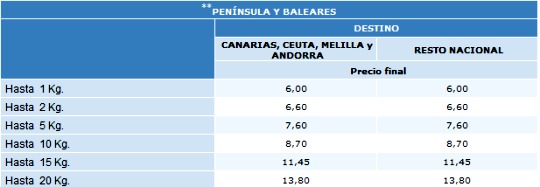| Captura de pantalla de la web de Correos |
Consideramos la función que al peso del paquete le asocia el precio que hay que pagar:
- Representa gráficamente la función anterior.
- ¿Es continua? ¿En qué puntos es discontinua?
- Calcula los siguientes límites:
, 
, 
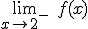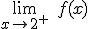y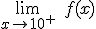 
. - Halla
.
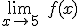Actividad
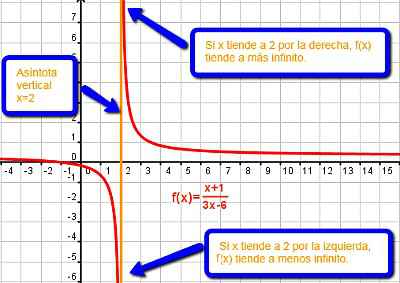
Una función tiene una asíntota vertical en el punto , de ecuación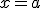 
si alguno de los límites laterales en ese punto es más o menos infinito.
En ese caso, la gráfica de la función se aproxima a la asíntota condicionada por el signo que tenga el infinito.
|
Imagen de elaboración propia |
En el siguiente vídeo de juanmemol puedes ver con detenimiento cómo se calculan los límites laterales de una función de proporcionalidad inversa en el punto en que se anula el denominar, es decir, el punto que corresponde a la asíntota vertical.
AV - Reflexión
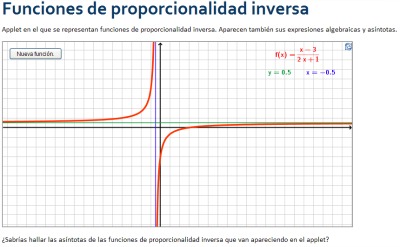
Si haces clic en la siguiente imagen, puedes acceder a una escena de GeoGebra en la que se representan funciones racionales. Te pedimos que halles las ecuaciones de las asíntotas de dichas funciones. Puedes comprobar si tu respuesta es correcta activando el controlador.
También debes calcular los límites laterales en el punto que corresponde a la asíntota vertical.
