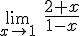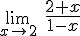2.1. Definición
Mira la imagen inferior. En ella aparece un caso particular de la escena de GeoGebra que hemos visto en un ejercicio resuelto. Recuerda, se nos pide que determinemos el primer trozo de una función definida por partes, de tal forma que la función resultante sea continua.
 |
| Imagen de elaboración propia |
Este primer trozo es una función constante 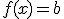 , cuando
, cuando 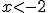 . ¿Cuánto valdrá
. ¿Cuánto valdrá 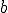 ? Esa es la pregunta a la que tenemos que contestar.
? Esa es la pregunta a la que tenemos que contestar.
Está claro que el punto culpable de que  pueda no ser continua es
pueda no ser continua es 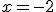 . Y para evitar que esto ocurra tendremos que saber cuanto vale
. Y para evitar que esto ocurra tendremos que saber cuanto vale  en
en 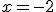 y en sus cercanías.
y en sus cercanías.
Sabemos que 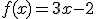 si
si 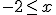 . Por tanto,
. Por tanto, 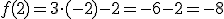 . Es decir,
. Es decir,  en
en 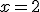 vale -8, y para los valores de
vale -8, y para los valores de 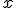 mayores que 2,
mayores que 2,  se acerca a -8.
se acerca a -8.
¿Cuánto tendrá que valer entonces 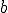 ? Eso es,
? Eso es, 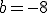 . De esa forma
. De esa forma  también será continua en
también será continua en 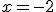 .
.
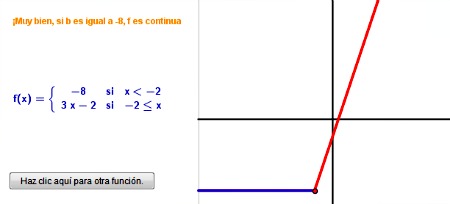 |
| Imagen de elaboración propia |
Estudiar el límite de una función en un punto consiste en saber cómo se comporta la función cuando nos acercamos a ese punto.
En el ejemplo anterior, para conseguir que  fuera continua en
fuera continua en 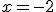 , hemos obligado a que el límite de
, hemos obligado a que el límite de  cuando
cuando 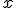 se acerca a -2 sea -8.
se acerca a -2 sea -8.
Escrito de forma más abreviada: 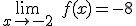
Importante
Si  se acerca a
se acerca a 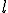 cuando
cuando 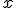 se aproxima al punto
se aproxima al punto  , diremos que
, diremos que 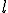 es el límite de
es el límite de  en el punto
en el punto  .
.
Lo anterior se expresa de la siguiente forma:
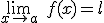
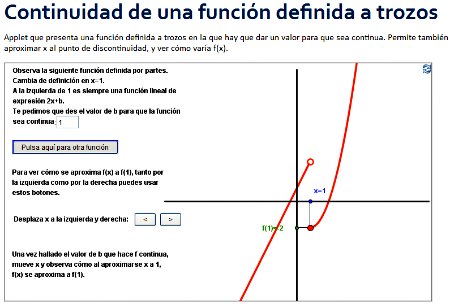
Si haces clic en la siguiente imagen, puedes acceder a una escena de GeoGebra muy similar a la anterior. En ella también se pide que determines un valor para que una función definida a trozos, sea continua en el punto 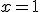 .
.
 |
| Imagen de elaboración propia |
La escena también te permite ver cómo varía  cuando
cuando 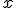 se acerca a 1. Puedes comprobar que, si la función aún no es continua en
se acerca a 1. Puedes comprobar que, si la función aún no es continua en 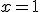 , los valores a los que se aproxima
, los valores a los que se aproxima  son distintos si lo hacemos para valores más pequeños que 1, o mayores. Por tanto no existe el límite de la función cuando
son distintos si lo hacemos para valores más pequeños que 1, o mayores. Por tanto no existe el límite de la función cuando 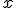 tiende a 1.
tiende a 1.
Pero, si repetimos el proceso cuando ya se ha conseguido que la función sea continua en 1, los valores a los que se aproxima  cuando
cuando 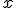 se acerca a 1, son iguales tanto si lo hacemos para valores menores o mayores que 1. En ese caso, sí existe el límite cuando
se acerca a 1, son iguales tanto si lo hacemos para valores menores o mayores que 1. En ese caso, sí existe el límite cuando 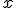 tiende a 1, y coincide con
tiende a 1, y coincide con 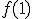 .
.
Repite la escena varias veces, hasta que entiendas lo que se ha explicado.
Importante
 , continua en un punto
, continua en un punto 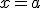 , es muy fácil. Se cumple que
, es muy fácil. Se cumple que 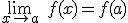 .
.
Esto facilita muchísimo el límite de una función en punto para las funciones continuas, que, como ya hemos visto, son la mayoría de las funciones elementales.
Calcular el límite de 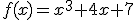 cuando
cuando 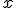 tiende, por
ejemplo, al punto -1, es muy fácil. Como
tiende, por
ejemplo, al punto -1, es muy fácil. Como  es una función polinómica,
por tanto continua en todo su dominio, basta con hallar
es una función polinómica,
por tanto continua en todo su dominio, basta con hallar 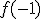 .
.
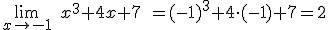
Ejemplo o ejercicio resuelto
Caso de estudio
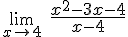
Actividad de rellenar huecos
Para terminar este apartado, veamos un vídeo de juanmemol en el que se explica un límite muy similar al ejercicio anterior: