2.3. Binomial
A Rafael, el investigador de la Estación Biológica de Doñana se le plantea el siguiente problema, de los diez huevos que han tenido Daisy y Donald este año, ¿cuántos polluelos saldrán adelante? ¿qué probabilidad hay de que, como ocurrió el año pasado, al menos ocho eclosionen?
Recuerda, los estudios de Rafael han llegado a la conclusión de que la probabilidad de que un huevo eclosione es de 0.66.
Vamos a ayudar a Rafael.
En primer lugar vamos a estudiar cuál es la probabilidad de que de los 10 huevos, solo eclosionen 8. Empezaremos numerando los huevos del 1 al 10, y viendo de cuántas maneras puede ocurrir lo anterior. La siguiente escena nos puede ayudar.
Puedes ver que las diferentes formas en que puedes eclosionar 8 de los 10 huevos anteriores no son más que las combinaciones de 10 elementos tomados de 8 en 8. Es decir:
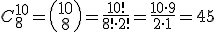
Es decir, 45 formas diferentes de que eclosionen 8 y 2 no.
La probabilidad de cada una de esas formas diferentes es igual a 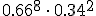 , ya que el que cada huevo eclosione o no, es independiente de que lo hagan los demás.
, ya que el que cada huevo eclosione o no, es independiente de que lo hagan los demás.
Por tanto, la probabilidad de que 8 de los 10 huevos eclosionen será igual a:

De la misma manera podemos ir calculando la probabilidad de que eclosionen 0, 1, 2,..., 7 huevos. Y así sabremos cuál es la probabilidad de que al menos 8 lo hagan.
A una distribución con características similares a las situaciones que hemos planteado con la eclosión de los huevos, el lanzamiento de las monedas o la máquina de Galton se la denomina Binomial.
Importante
Diremos que una distribución 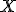 es binomial, si cumple las siguientes características.
es binomial, si cumple las siguientes características.
- Es un experimento aleatorio que se repite n veces de modo independiente.
- Cada vez que se realiza el experimento solo pueden darse dos sucesos al estilo de la Bernouilli, éxito o fracaso.
- La suma de las probabilidades del éxito y fracaso debe ser 1. Normalmente p es la probabilidad del suceso éxito, y q=1–p la del suceso fracaso.
La distribución la denotaremos por 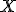 es B(n,p).
es B(n,p).
Su función de probabilidad es:
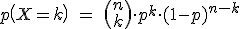
Donde k es el número de éxitos de los queremos conocer la probabilidad. Por tanto 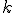 puede tomar los valores 0, 1, 2,..., n.
puede tomar los valores 0, 1, 2,..., n.
Caso de estudio
Vamos a estudiar las probabilidades de una máquina de Galton de 8 alturas.
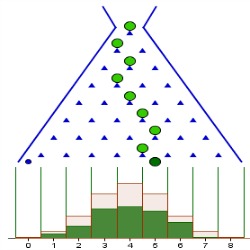 Imagen de elaboración propia |
Repasemos si cumple las condiciones para ser una distribución binomial. El experimento se repite 8 veces y son independientes, los resultados son izquierda (éxito) o derecha (fracaso) y la suma de sus probabilidades es 1, ya que ambos tienen probabilidad 0.5.
Estamos ante una distribución 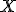 , binomial B(8, 0.5).
, binomial B(8, 0.5).
Calcularemos 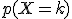 , es decir que la bola en su recorrido haya ido
, es decir que la bola en su recorrido haya ido 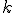 veces a la izquierda y
veces a la izquierda y 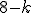 veces a la derecha, donde
veces a la derecha, donde 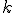 = 0, 1,... , 8.
= 0, 1,... , 8.
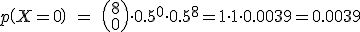
|
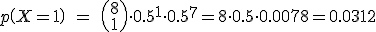 |
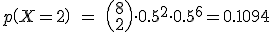 |
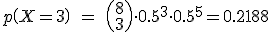 |
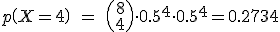 |
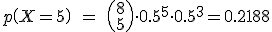 |
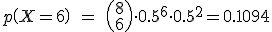 |
 |
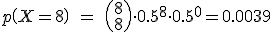 |
Si construimos una tabla con las funciones de probabilidad, obtendremos la siguiente gráfica.
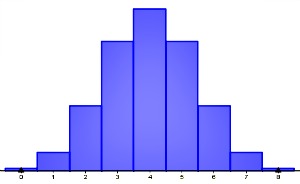 Imagen de elaboración propia |
Se puede apreciar que la gráfica es simétrica y se concentra en la probabilidad de 4 izquierdas y 4 derechas. ¿Recuerdas cómo se distribuían las bolas en las diferentes repeticiones de la máquina de Galton en el vídeo del principio del tema?
Actividad de rellenar huecos

|
| Imagen de elaboración propia |
Se lanzan 8 monedas al aire, y queremos saber cuál es la probabilidad de obtener más de 3 cruces.
Completa los siguientes espacios en blanco para dar una solución al problema planteado.
En la siguiente escena de Geogebra podemos calcular probabilidades de una distribución binomial de una manera simple. Basta con que demos los valores p, n y k correspondientes.
AV - Pregunta Verdadero-Falso
En todos los apartados de este ejercicio consideraremos que tenemos una distribución binomial, B(5;0.2)
Con la ayuda de la escena anterior, o bien realizando los cálculos de manera manual, calcula las probabilidades indicadas y selecciona Verdadero o Falso según corresponda.
Retroalimentación
Verdadero
Es Verdadero.
Basta configurar en la escena los siguientes valores: p=0,2; n=5 y k=3.
Retroalimentación
Falso
Es falso.¡No se puede calcular, porque es imposible obtener k=6 éxitos al realizar n=5 experimentos!
Retroalimentación
Falso
Es falso.Por definición de Función de Distribución de una variable aleatoria discreta tenemos que: "la probabilidad de que X sea menor o igual que 3 es igual a la suma de las probabilidades de los valores menores o iguales que 3", es decir,
P(X≤3)= P(X=3) + P(X=2) + P(X=1) + P(X=0) = 0,0512 + 0,2048 + 0,4096 + 0,32768 = 0,99328
Importante
Si 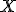 es una variable aleatoria binomial, B(n,p), tendremos que:
es una variable aleatoria binomial, B(n,p), tendremos que:
Su esperanza matemática o media es 
La varianza es 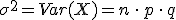
Y la desviación típica es la raíz cuadrada de la varianza 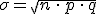
En el siguiente vídeo del canal de juanmemol puedes ver cómo hallar la esperanza y la desviación típica de una variable aleatoria binomial:
Y en este otro enlace de la página de Vitutor, puedes repasar la distribución binomial y ver algunos ejercicios resueltos.