2.2. Números combinatorios
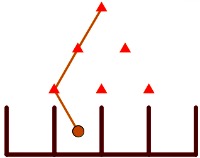
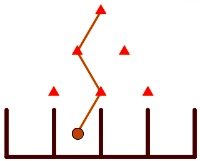
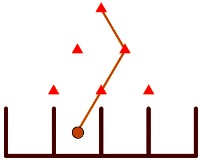
¿En una máquina de Galton de tres alturas, cuántos son los recorridos posibles en los que la bola cae dos veces a la izquierda y una a la derecha?
|
|
|
| Imágenes de elaboración propia |
||
Son tres y podríamos sintetizarlos como I-I-D, I-D-I y D-I-I. Expresado de otro modo, que las dos izquierdas sean en los pasos 12, 13 ó 23.
¿De cuántas formas nos pueden salir dos cruces si lanzamos tres monedas?
|
|
|
| Imágenes de elaboración propia | ||
¿Qué casualidad, también son tres? Y podríamos representarlos de forma esquemática como XXC, XCX y CXX. O en función del lugar que ocupan las cruces: 12, 13 y 23.
Se repite el esquema de la máquina de Galton.
En el caso de que fuera una máquina de cuatro alturas y nos hiciéramos la misma pregunta, ¿cuántos son los recorridos posibles en los que la bola cae dos veces a la izquierda y dos a la derecha?, tendríamos las siguientes posibilidades:
| IIDD |
IDID |
IDDI |
DIID | DIDI |
DDII |
| 12 | 13 | 14 | 23 | 24 | 34 |
Es decir, 6 recorridos. Si nos fijamos en la fila inferior, hemos escrito todas las formas posibles de agrupar 4 números de 2 en 2.
Caso de estudio
Si escribimos las 10 posibles formas de que salgan 2 cruces al lanzar 5 monedas, en función del lugar que ocupan, nos quedaría: 12, 13, 14, 15, 23, 24, 25, 34, 35 y 45. Que no son más que todas las formas posibles de agrupar 5 números tomados de 2 en 2.
Hasta ahora hemos hallado "las formas de agrupar m números tomados de n en n", a mano. Pero si n y m son grandes, esa labor puede ser tediosa y casi agotadora.
Importante
Llamaremos combinaciones de m elementos tomados de n en n al número de agrupaciones posibles de esos m elementos formadas por n de ellos.
Las denotaremos como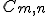 
, 
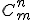o 
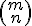. A esta última expresión también se le llama número combinatorio de m sobre n.
Calcularemos el número de combinaciones de m elementos tomados de n en n, usando la siguiente fórmula:
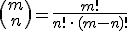
Donde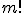 
se denomina factorial de m, y se calcula como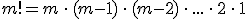 
|
| Imagen en Flickr de Leo Reynolds bajo CC |
Apliquemos las definiciones anteriores a las posibles formas de obtener 2 cruces al lanzar 5 monedas. Ya sabemos que son 10, e incluso las hemos descrito:
12, 13, 14, 15, 23, 24, 25, 34, 35 y 45
Pero vamos a usar los números combinatorios para hallar su número.
Lo que queremos calcular es el número de formas en que podemos agrupar 5 elementos tomados de 2 en 2, es decir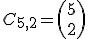 
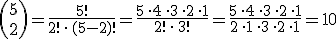
¡Uf, qué lío! Menos mal que las nuevas tecnologías nos alivian de la tediosa y pesada carga de factoriales y multiplicaciones.
Por ejemplo, con una calculadora científica de las actuales es posible hallar el factorial de un número o calcular números combinatorios. En las imágenes inferiores se puede apreciar cómo calcular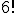 
o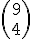 
con la fx-82ES de Cassio.
|
|
| Imágenes de elaboración propia |
|
Caso de estudio
Si haces clic en la siguiente imagen podrás acceder una la página del Proyecto Descartes del MECD con escenas que permiten calcular fácilmente factoriales de números y números combinatorios.
|
| Imagen de elaboración propia |
AV - Reflexión
En una clase de 24 estudiantes queremos seleccionar un grupo de seis para que representen a la clase en un concurso de elaboración de figuras geométricas, que se realizará en el Instituto con motivo de la semana de la ciencia.
a) ¿Cuántas combinaciones posibles hay de formar el grupo?
b) ¿De cuántas maneras pueden hacerse los grupos si se pone la condición de que la alumna más creativa de la clase debe pertenecer siempre a ellos?
