1.1. Definición
Es casi obligatorio jugar a los dados cuando se habla de probabilidad, de hecho se considera que el origen de esta rama de las matemáticas se encuentra en el deseo de encontrar reglas a este juego.
En la siguiente escena de GeoGebra creada por el profesor Jesús Fernández, se simula el lanzamiento de dos dados. Realiza varios lanzamientos y piensa un poco cuál será el espacio muestral que se obtiene.
Caso de estudio
Del espacio muestral del ejercicio anterior vamos a fijarnos en la suma de los números que aparecen en los dados. A cada resultado obtenido le asociamos un número, la suma de las caras superiores. Si han salido los números 4 y 3, el suceso es (3, 4), y la suma sería 7.
A este tipo de aplicación se le denomina variable aleatoria.
Importante
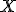, a una aplicación que asocia un número real a cada elemento de un espacio muestral.
Actividad de rellenar huecos
|
| Imagen en Flickr de Catwomancristi bajo CC |
Si X es la variable aleatoria que asocia la suma de las caras superiores al experimento aleatorio de lanzar dos dados, te pedimos que completes los huecos que aparecen en las siguientes afirmaciones.
No todas las variables aleatorias se aplican a un juego de azar, otras actúan sobre estudios estadísticos, por ejemplo, el tiempo de espera para una intervención quirúrgica. Observa la noticia del diario digital El Adelanto.com:
 Imagen de elaboración propia |
El espacio muestral son los enfermos que se encuentran en lista de espera para una operación, y la variable aleatoria es la que asocia a cada enfermo el tiempo que tendrán que esperar.
En este caso, los valores que toma la variable aleatoria pueden ser números decimales, a diferencia de la suma de la puntuación obtenida al lanzar dos dados, que son números enteros.
Importante
Diremos que una variable aleatoria es discreta si los valores que toma son números enteros.
Llamaremos variable aleatoria continua a la que toma valores en un intervalo de números reales.
El lanzamiento de los dos dados corresponde a una variable aleatoria discreta, en tanto que el tiempo de espera es de tipo continuo.
Este tema lo dedicaremos a las variables aleatorias discretas, dejando el siguiente para tratar las continuas.
Pregunta de Elección Múltiple
Solution
Solution
Solution
Solution
Para terminar, veamos qué tipo de variable aleatoria está asociada a la máquina de Galton.
Presentación de elaboración propia