4.2. Función racional
Importante
Si tenemos una función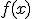 
decimos que es una función racional si tiene la forma 
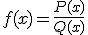donde 
y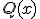 
son funciones polinómicas. En este caso tenemos que:
1.- El dominio de la función 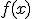son todos los valores para los que 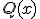es distinto de cero.
2.- Lo más normal es que tenga intervalos de crecimiento y de decrecimiento.
3.- Un caso particular de función racional lo tenemos en las funciones hiperbólicas cuya forma es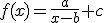 
en la siguiente ventana puedes observar la representación gráfica de este tipo de funciones.
Ejemplo o ejercicio resuelto
 |
| Fotografía de Launa Fischer Ferreira tomada del Banco de Imágenes del ITE. |
En la empresa de Amelia, Lucas, el programador informático de una de las máquinas que están automatizando está teniendo muchos problemas con la misma. Según sus cálculos, cuando la persona que está manejando la máquina introduce un número cualquiera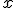 
, la máquina debe seguir un determinado proceso que la lleva a hacer el cálculo siguiente: 
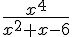, pero Lucas se ha dado cuenta de que a veces tiene problemas para hacerlos. Por este motivo, Lucas está intentando saber si es lo mismo introducir un número negativo que uno positivo. Para este menester, está viendo los posibles valores que toma cuando se introduce el cero. Intenta echarle una mano averiguando los números para los que puede tener problemas. Ayúdale a saber si puede intercambiar los números positivos y negativos como pretende y a saber los valores en el cero y cuando la operación resulta ser cero.
Representa la función en la ventana interactiva que encuentras más abajo y observa si las propiedades de la gráfica que resulta se corresponden con las que has calculado.
Te aconsejamos a la hora de representarla en la ventana interactiva que apliques zoom tomando xmín=-25, xmáx=25, ymín=-10, ymáx=25 para poder contemplar mejor la gráfica.