1.2. Moda y mediana
 |
| Imagen de José Goulão con licencia Creative Commons |
¿Recuerdas el ejemplo anterior de la valoración de nuestro líder político? Volvamos a ver los resultados obtenidos en la encuesta:
| Puntuación | 0 | 1 | 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| N.º de personas |
12 |
38 | 62 | 97 | 160 | 130 |
65 |
18 |
11 |
6 |
1 |
Si bien la media es el valor central más representativo de una muestra, no es el único valor central que podemos calcular. También podemos ver cuál es el dato que más se repite, en nuestro caso, cuál es la puntuación que más personas han elegido para valorar al líder político. En el ejemplo este valor es 4. Este dato es la moda de la variable estadística.
Importante
Se llama moda de una variable estadística al valor de la variable que presenta mayor frecuencia absoluta. La moda se representa por M0.
Si la variable es discreta, el cálculo de la moda no presenta ninguna dificultad, únicamente observamos las frecuencias absolutas en la tabla, vemos cuál es la mayor y la moda será el valor de la variable correspondiente a dicha frecuencia. Puede que haya más de un valor máximo, en este caso la distribución será bimodal (si hay dos), trimodal (si hay tres), ...
Si la variable es continua los valores se agrupan en intervalos, por lo que tendremos un intervalo modal que será el de mayor frecuencia absoluta. No obstante, si consideramos que los datos están uniformemente distribuidos podemos calcular un valor concreto para la moda que vendrá dado por la siguiente fórmula:
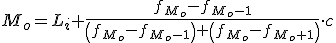
Donde Li es el límite inferior del intervalo modal, las frecuencias absolutas corresponden al intervalo modal, al anterior y al siguiente y c es la amplitud de dicho intervalo.

|
| Imagen de IowaPolitics.com con licencia Creative Commons |
Además de la moda, podemos calcular el valor que está justamente en el centro de todos los datos una vez que están ordenados. En nuestro ejemplo tenemos 600 datos, sería interesante conocer cuál es el valor que deja 300 datos menores que él y otros 300 mayores que él. Este dato es la mediana. Para calcularla nos vamos a ayudar de la tabla de frecuencias, a la que añadiremos la columna de la Frecuencia acumulada (Fi). Esta frecuencia se obtiene sumando todas las frecuencias absolutas hasta el dato en el que nos encontramos.
| xi | fi |
Fi |
| 0 | 12 |
F1=f1=12 |
| 1 |
38 | F2=f1+f2=50 |
| 2 |
62 |
F3=f1+f2+f3=112 |
| 3 |
97 |
209 |
| 4 |
160 |
369 |
| 5 |
130 |
499 |
| 6 |
65 | 564 |
| 7 |
18 |
582 |
| 8 |
11 | 593 |
| 9 |
6 | 599 |
| 10 |
1 | 600 |
| N=600 |
Para el cálculo de la mediana lo primero que hay que hacer es construir la tabla de frecuencias anterior. A continuación, calculamos la mitad del número de datos 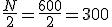
- Si N es impar la mediana corresponderá al xi correspondiente al primer Fi que supere ese valor.
-
Si N es par:
- Si exite algún valor de la columna Fi que es igual a
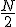 , la mediana es la media entre el xi correspondiente a ese Fi y el siguiente, xi+1.
, la mediana es la media entre el xi correspondiente a ese Fi y el siguiente, xi+1. - En caso contrario, la mediana será el xi que se corresponda con el primer valor de Fi que supere a
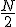 .
.
- Si exite algún valor de la columna Fi que es igual a
En nuestro caso la mediana es 4,porque 4 es el primer valor de la variable cuya frecuencia acumulada supera el valor de 300.
Importante
Hemos visto el cálculo de la mediana cuando la variable era discreta. Para el caso de la variable continua, si usamos intervalos se realiza de la misma forma y se obtiene el intervalo mediano. No obstante, si consideramos que los datos se distribuyen uniformemente se puede calcular el valor exacto de la mediana mediante la siguiente fórmula:
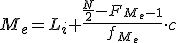
AV - Reflexión
Los jugadores de un equipo de baloncesto se clasifican por la altura según la siguiente tabla
| Alturas | Número de jugadores |
|
[1'70,1'80) [1'80,1'90) [1'90,2'00) [2'00,2'10) |
3 4 5 3 |
Hallar la media, el intervalo modal, la moda, el intervalo mediano y la mediana
En la siguiente página puedes encontrar ejercicios resueltos de cálculo de la media, mediana y moda de una serie de datos.
Para saber más
Además de las medidas de centralización existen otras medidas, las medidas de posición. Éstas, como ocurre con la mediana, nos dan el valor que deja un porcentaje de la población a su izquierda. La mediana puede considerarse también una medida de posición, ya que deja el 50% de la población a su izquierda.
Estas medidas son los cuartiles, los deciles y los percentiles. Realmente los cuartiles corresponden al percentil 25 y 75, pues dejan respectivamente el 25% y el 75% de la población a su izquierda. Vamos a ver en el siguiente vídeo como realizar el cálculo del percentil.
AV - Pregunta Verdadero-Falso
Retroalimentación
Verdadero
Es justo para lo que sirven.Retroalimentación
Falso
No es posible cuando los datos son cualitativos.Retroalimentación
Falso
Para el cálculo de la moda sólo es necesario conocer el valor que aparece más veces.Retroalimentación
Verdadero
La mediana deja el 50% de los datos a su izquierda, por lo tanto, corresponde con el valor de P50Retroalimentación
Verdadero
Los parámetros de centralización suelen situarse hacia el centro del conjunto de datos ordenados