4.1 Formulación matemática de la ley

Imagen en COMMONS.WIKIMEDIA de Luestling bajo licencia CC

La ley de la Gravitación Universal predice que la fuerza ejercida entre dos cuerpos de masas y separados una distancia es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que separa sus centros, es decir:

 

F es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.

G es la constante de la Gravitación Universal. Hablaremos de ella con más detalle en el siguiente apartado.

Newton pudo deducir esta ley basándose en sus leyes de la Dinámica.

Partiendo del movimiento circular de un planeta alrededor del Sol, y teniendo en cuenta variables de los movimientos circulares, el módulo de la fuerza de atracción gravitatoria entre ambos se puede expresar como:

Si la expresión anterior se multiplica por R²se tiene:

 

Teniendo en cuenta la tercera ley de Kepler , la expresión anterior puede escribirse como:

La constante K es proporcional a la masa de cuerpo sobre el que se orbita. Esta constante puede englobarse en otra constante G, que muestre esa proporcionalidad:

 Por tanto, la expresión de la fuerza quedaría como:

 

Esta animación puede aclarar algo más esta ley.

Imagen en COMMONS.WIKIMEDIA de FJGAR bajo licencia CC

Si lees atentamente el enunciado de la ley, podrás intuir que la expresión matemática anterior sólo representa parte de la situación. Implícitamente, en la misma se atisba que debe tener cierta importancia la dirección, ya que se indica que la distancia es del centro al centro de cada cuerpo.

Por tanto, la fuerza sería una magnitud vectorial, por lo que su definición correcta sería:

donde  representa un vector unitario en la dirección de la recta que une los centros de ambos cuerpos.

Mediante la visualización del siguiente video, puedes repasar el concepto de "vector".

Video de Tareasplus publicado en Youtube.

 Puedes encontrar información más ampliada sobre los vectores y sus operaciones, haciendo clic en la flecha.

 

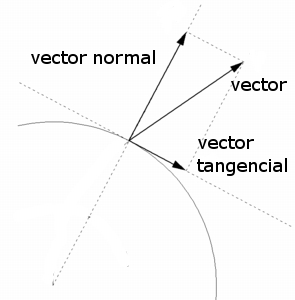
Existen algunos términos acerca de los vectores muy empleados en Física. Uno de ellos ya lo hemos visto antes; es el vector unitario. Pero también hay otros términos relacionados con los vectores y que tienen sentido en los movimientos circulares, como son el vector normal y el vector tangencial.

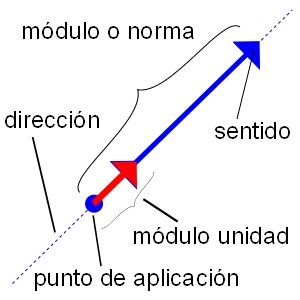
Si observas las siguientes imágenes verás las representaciones de los vectores unitarios y de vectores normales y tangenciales.

Imagen en COMMONS.WIKIMEDIA de FJGAR bajo licencia CC	Imagen en COMMONS.WIKIMEDIA de FJGAR bajo licencia CC

 

Un vector unitario se puede  definir como aquel que tiene por norma o módulo la unidad y, por tanto, se puede construir un vector unitario partiendo de cualquier vector, sólo se tiene que dividir por el módulo de éste.

Por otro lado, un vector normal es llamado al vector que con respecto a una referencia forma un ángulo de 90º con respecto a la misma. Si el ángulo formado con respecto a tal referencia toma valor nulo se le denomina al vector tangencial.