4.1. Póngame cuarto y mitad
 |
 |
 |
 |
 |
 |
| Fotografías en ISFTIC bajo CC | ||
En nuestra actividad cotidiana utilizamos habitualmente términos como mitad, un tercio, un cuarto... Se trata de expresiones que designan a partes de un todo. Las conocemos como fracciones. El origen de las fracciones, o quebrados, es muy remoto.
Pre-conocimiento
La fracciones ya eran conocidas por los babilonios que las utilizaron teniendo como único denominador al número 60, los egipcios, por su parte, las emplearon con sólo el 1 como numerador (por ejemplo, si querían representar 5/8 escribían: 1/2 y 1/8, considerando que 1/2 equivale a 4/8) y los griegos que marcaban con un acento el numerador, y con dos el denominador. Pero el nombre de fracción se lo debemos a Juan de Luna, que tradujo al latín, en el siglo XII, el libro de aritmética de Al-Juarizmi. De Luna empleó la palabra «fractio» para traducir la palabra árabe «al-Kasr», que significa quebrar, romper.
En la historia, es posible distinguir dos motivosprincipales por los que fueron inventadas las fracciones:
- El primero de ellos fue la existencia de divisiones inexactas. Por ejemplo: 5/4 representa 5:4.
- Un segundo motivo por el cual se crearon las fracciones resultó de la aplicación de unidades de medida de longitud. Para realizar las mediciones de trozos, se tomaba otro trozo como unidad de medida, y se veía las veces que contenía en el otro. Como no siempre cabía de manera exacta, se dividía el trozo que servía de unidad en partes iguales y más pequeñas, para que el resultado fuera exacto. Este resultado de la medición se expresaba en fracción.
Antes de entrar en materia, hacemos un primer acercamiento visual con el siguiente video:
Una vez que ya tengas clara la idea de fracción, ahora toca recordar cómo se opera con ellas. Para ello te ofrecemos los siguientes recursos:
1) Una presentación con contenidos teóricos y algún ejemplo práctico:
2) Una unidad muy completa del proyecto EDAD, dónde no sólo encontrarás teoría, también ejercicios resueltos:
3) Unos vídeos con ejemplos concretos, en los que se practican las operaciones combinadas con números racionales, incluyendo potencias:
|
|
|
|
|
|
Caso de estudio
Caso de estudio
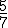del grupo son chicas y en total son 28. ¿Cuántas chicas hay en esa clase?
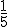de su dinero en la entrada para un coche, 
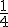en comprarse los muebles que necesita, la décima parte de sus ahorros en un ordenador y 
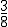de los mismos en liquidar lo que le falta para terminar de pagar su casa,
aún le quedarán 375 €. "No está nada mal", piensa ella. Por cierto,
¿cuánto dinero tiene Paqui?
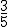de su dinero en ropa, 
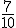de lo que aún le quede en música y 30 € en un libro. Lo que le sobre se lo
regalará a su hermana. ¿Es muy generosa con su hermana?
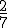de todos los exámenes, hoy piensa corregir 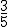de los que le quedan, y así para mañana sólo le restarán 8. ¿Cuántos alumnos/as se presentaron al examen?.
Pregunta de Elección Múltiple
Objetivos
Una fracción se puede convertir en un número decimal, basta con dividir el numerador entre el denominador. Puede ocurrir que el decimal resultante sea: exacto (por ejemplo, 
), periódico puro (por ejemplo, 
) o periódico mixto (por ejemplo, 
).
Los números decimales exactos, los periódicos puros y los periódicos mixtos se pueden convertir en fracciones.
En el siguiente enlace tienes una actividad en la que puedes aprender a transformar estos decimales en fracciones, es decir, hallar la fracción generatriz.
Pre-conocimiento
En la mitología egipcia, Horus era hijo de Osiris, el dios que fue asesinado por su propio hermano Seth. Horus intentó vengar a su padre, y en sus combates con Seth perdió el ojo izquierdo. Pero Thot, el dios de la sabiduría, la música y la escritura le devolvió la vista con un ojo de cualidades mágicas. ¿Sabías que los signos de las fracciones mayores fueron tomados de las partes que formaban el jeroglífico de ese ojo?
Puede completar esta información en el siguiente artículo de la wikipedia.