3.1. Repaso del concepto de número combinatorio
La Unidad 1 de esta materia está dedicada a estudiar distintas clases de números: naturales, enteros, racionales, irracionales y reales. Pero, como decían los famosos dibujos animados: "no se vayan todavía, aún hay más..."
¿Todavía más? Pues sí. En este apartado vamos a ver dos nuevos tipos: los números factoriales y los números combinatorios.
Como cualquier otro objeto matemático, su misión principal es ayudarnos a resolver problemas. En este caso, los números combinatorios nos ayudarán a trabajar con las distribuciones normales y a calcular probabilidades con este tipo de distribuciones.
 |
|
Combinatoria de wikimedia commons con licencia by-2.0-deed |
Combinaciones
Se define el factorial de un número entero positivo, n, como el producto de todos los números menores o iguales que él. Se escribe n!
Por convenio: 0! = 1
Ejemplo: 5! = 5 · 4 · 3 · 2 · 1 = 120
Los números factoriales son necesarios para definir los números combinatorios.
Actividad
Si tenemos dos números enteros positivos m y n (con n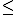 
m ), se define el número combinatorio m sobre n con la siguiente expresión:
Su resultado es un número positivo que indica el número de combinaciones distintas de n elementos que se pueden formar con m elementos. Los números combinatorios cumplen una serie de propiedades. Indicamos algunas de ellas:
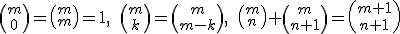
En la siguiente escena de Geogebra puedes practicar calculando factoriales y números combinatorios. Practica con algunos números de este tipo que tú te propongas, haz los cálculos en papel y comprueba a continuación en la escena que el resultado es correcto.
Por ejemplo, puedes ver cuánto vale el factorial de 0 ó un número m cualquiera sobre 0,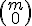 
.
|
Escena de elaboración propia alojada en Geogebra tube |
AV - Reflexión
En una clase de 24 estudiantes, queremos formar un grupo de 6 que representen a dicha clase en un concurso de elaboración de fíguras geométricas que se realizará en el instituto con motivo de la semana de la ciencia.
(a) ¿Cuántas maneras, combinaciones posibles, hay de formar el grupo?
(b) ¿De cuántas maneras puede hacerse el grupo sabiendo que un alumno muy creativo de la clase, Jesús, debe estar de manera fija en el grupo?
 |
|
Triángulo de Sierpinski con material reciclado. |
A continuación se incluye un pequeño vídeo donde se muestra como calcular números combinatorios, de un modo sencillo, con Wiris.
