3.2. Medidas de dispersión

Imagen en Flickr de Håkan Dahlström bajo CC

Al igual que pasa en el mundo, las variables estadísticas no siempre están bien repartidas, de tal forma que la media puede no ser representativa si hay valores dispares que le afecten. Para eso tenemos las medidas de dispersión, que nos informan de la concentración de esos datos dentro de la variable.

Las medidas de dispersión nos informan de hasta qué punto las medidas de centralización son representativas como síntesis de la información.

Las medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central.

Estudiaremos a continuación el recorrido, la desviación media, la varianza, la desviación típica y el coeficiente de variación.

 

Recorrido

El recorrido de una variable es la diferencia entre el mayor y menor valor que toma esa variable. Se representa por 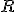. En el caso de tener los datos agrupados por intervalos, el recorrido sería la diferencia entre el extremo superior del mayor intervalo y el extremo inferior del menor intervalo (no intervienen las marcas de clase).

 

Desviación media

Se define el parámetro desviación media como la suma de las diferencias entre los valores y la media, en valor absoluto, dividido por el número total de valores.

 

 

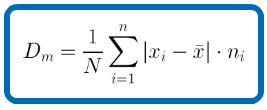
Imaginemos que estamos interesados en comprar en bolsa acciones de una determinada empresa. Para saber si es una inversión segura, investigamos la evolución del precio de las acciones en el último año. Por supuesto, hemos calculado previamente cuál ha sido el precio medio de las acciones y mirando el resto de los valores podremos decir que si muchos días el precio ha estado alejado de la media (por debajo o por encima), diremos que la inversión es arriesgada o volátil. Y por el contrario, si la mayoría de los días el precio ha estado cerca de la media diremos que la inversión es segura.

La medida estadística que nos indica esta variación de los datos respecto de la media es la varianza.

Varianza y desviación típica

La varianza se define como la media aritmética de los cuadrados de las desviaciones de cada valor respecto a la media. Se representa por 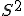, y se calcula mediante la fórmula:

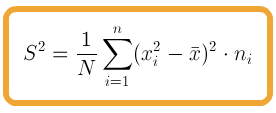
La desviación típica es la raíz cuadrada positiva de la varianza. Se representa por .

Aunque tanto la varianza como la desviación típica son medidas de la variación con respecto a la media y tienen un significado semejante, la desviación típica se utiliza con más frecuencia porque se expresa en las mismas unidades que los valores de las variables. Al contrario que la varianza, cuyos valores se expresan en unidades al cuadrado.

Haciendo algunos cambios y realizando algunos cálculos podemos obtener una fórmula más operativa para la varianza:

 

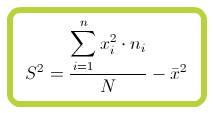
La varianza y la desviación típica también podemos encontrarla representadas como 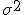y 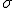respectivamente.

A continuación un ejemplo en un contexto real:

 

Cuando queremos comparar la dispersión entre dos poblaciones distintas, es muy útil la siguiente medida:

Coeficiente de variación

El coeficiente de variación se define como el cociente entre la desviación típica y la media. Se representa por CV.

 

 

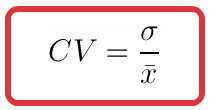
El coeficiente de variación se suele expresar en porcentajes: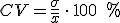

Cuanto mayor sea el coeficiente de variación, más dispersión hay en la variable y menos representativa es la media.

El coeficiente de variación es una medida independiente de las unidades de medición, ya que es el cociente de la desviación típica y la media, y ambas se miden en las mismas unidades.