3.1. Medidas de centralización
Las medidas de centralización son datos que representan de forma global a toda la población, y en torno a los cuales están agrupados todos los valores.
Estas medidas de centralización no son conceptos desconocidos, muy al contrario, aparecen continuamente en nuestra vida. Por ejemplo:
- A los niños pequeños, uno de los primeros conceptos que se les enseña son los tamaños. A muy corta edad aprenden la diferencia entre grande, mediano y pequeño.
- Hoy en día ir a la moda es una de las preocupaciones de mucha gente. Para no quedarte desfasado tienes que estar a la moda, es decir, en este caso, vestirte de la misma forma que mucha otra gente.

|
| Imagen en Flickr de laverrue bajo CC |
- ¿Sabías que van a situar dos radares seguidos y a cierta distancia, para de esa forma calcular la velocidad media a la que circulamos, y así poder comprobar si infringimos la ley?
Actividad
Notación
Llamaremos 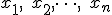 a los datos si la distribución está ordenada por elementos, o a las marcas de clase si está ordenada por intervalos.
a los datos si la distribución está ordenada por elementos, o a las marcas de clase si está ordenada por intervalos. 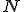 al número total de datos, que coincide con la suma de las frecuencias absolutas,
al número total de datos, que coincide con la suma de las frecuencias absolutas, 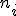 . Recuerda que
. Recuerda que 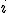 va desde
va desde 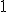 hasta
hasta 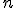 , que es el número de datos distintos.
, que es el número de datos distintos.
Media aritmética
Se calcula al sumar todos los elementos y dividir por el número total de elementos de la población, o lo que es lo mismo, si los datos vienen en una tabla de frecuencias, se multiplica cada dato por su frecuencia absoluta y se suman los resultados obtenidos, y este resultado se divide por el número total de datos. Se denota por 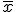 o por
o por 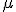 .
.
Si los datos vienen agrupados en intervalos, se multiplica la marca de clase por su frecuencia, se suman los resultados obtenidos y este total se divide por el número de datos.
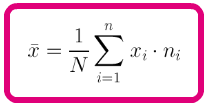
Propiedades
- Solo se puede obtener con datos cuantitativos.
- Puede no coincidir con ninguno de los datos, y se encuentra entre el menor y el mayor de los datos de la distribución.
- Cuando aparecen valores extremos y poco significativos la media puede que no sea representativa.
- Es única. Solo existe una por cada distribución.
 |
| Imagen de elaboración propia |
Moda
En el caso de una variable no agrupada, se define como el valor que más se repite entre los datos de que disponemos, es decir, es el dato que tiene mayor frecuencia absoluta. Vamos a representarla por  .
En el caso de una variable agrupada en intervalos de igual amplitud se busca el intervalo con mayor frecuencia, al que llamaremos, intervalo modal. Dentro del intervalo modal se suele tomar como moda el punto medio del intervalo (marca de clase).
.
En el caso de una variable agrupada en intervalos de igual amplitud se busca el intervalo con mayor frecuencia, al que llamaremos, intervalo modal. Dentro del intervalo modal se suele tomar como moda el punto medio del intervalo (marca de clase).
Propiedades
- La moda es el único estadístico que puede utilizarse con cualquier tipo de variable. En concreto es el único parámetro que tiene sentido calcular en las variables cualitativas.
- Tiene además la particularidad de ser el único parámetro estadístico que puede tomar más de un valor. Por ejemplo, una familia muy numerosa, con ascendencia de partos múltiples tiene 6 hijos cuyas edades son 3, 3, 6, 10, 10, 14. Entre esos datos, la moda correspondería a los valores 3 y 10 ya que ambos se repiten dos veces.
|
|
|
Mediana datos impares |
|
|
|
Mediana datos pares |
| Imágenes en Wikipedia bajo CC |
Mediana
Es el valor de la variable que divide a la serie de datos ordenados en dos partes iguales. Si los datos no están agrupados por intervalos, tenemos dos casos:
- El número de datos de los que disponemos es impar, en cuyo caso se ordenan en orden creciente y la mediana es el término que ocupa el lugar central.
- Si el número de datos es par, la mediana es la media aritmética de los dos valores centrales.
Se representa por 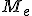 .
.
Propiedades
- Solo se puede obtener para datos cuantitativos.
- Es única, y puede no ser un dato de la distribución.
Si los datos están agrupados por intervalos, hablamos del intervalo mediano o central que es aquel donde se encuentre el o los valores centrales. Es posible utilizar una fórmula para precisar un valor para la mediana dentro del intervalo mediano. En el siguiente enlace puedes encontrarla:
Caso de estudio
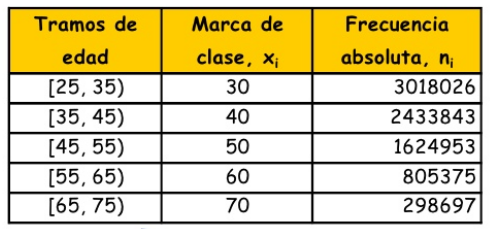
La siguiente distribución agrupada por intervalos, es fruto de una encuesta sobre la participación de la población adulta española en actividades de aprendizaje (EADA 2007):
|
Calcula las medidas de centralización asociadas.
Caso de estudio
 |
Curso 2011/2012
En una urbanización se ha realizado un estudio sobre el número de personas que habitan en cada piso y se obtienen los siguientes datos:
| Personas |
1 |
2 |
3 |
4 |
5 |
| Pisos |
20 |
60 |
52 |
35 |
18 |
a) ¿Cuántos pisos hay en la urbanización?
b) Determine la media y la moda de la distribución.
