2.1. Frencuencia y tablas
|
| Imagen en Flickr de Andy.Schultz bajo CC |
Las personas a veces tendemos a acumular objetos, ropa... y para organizarnos las ordenamos en armarios, estanterías, etc. De esta forma, sabemos qué tenemos y dónde lo tenemos. Pues bien, cuando realizamos un estudio estadístico muchos son los datos que obtenemos sin ningún tipo de orden.
Pero de esta cantidad de datos, ¿podemos obtener alguna información?
Parece lógico pensar que ordenándolos y posteriormente encontrando semejanzas podamos agruparlos y obtener, de esta forma, una información que pueda describirnos la población escogida.
 |
| Imagen de elaboración propia |
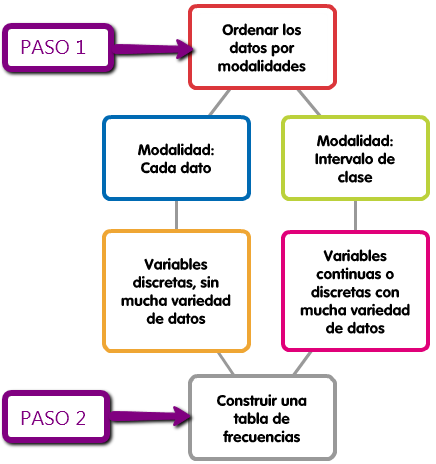
El primer paso para ordenar estos datos es definir las distintas modalidades según los resultados obtenidos.
Esto podemos hacerlo de dos formas:
- Ordenarlos por elementos. En general, optamos por esta técnica en variables discretas, en los que la variedad de datos no es muy amplia (variedad no cantidad). Las modalidades serían todas las posibles repuestas.
- Ordenarlos por intervalos. En general, optamos por esta técnica en variables cuantitativas continuas o en variables discretas en las que hemos obtenido datos muy variados. Estos intervalos se reciben el nombre de intervalos de clase, en los cuales se agruparán los datos observados en una muestra. Así, cada intervalo es considerado como una modalidad. Una vez construidos los intervalos de clase, se elige un representante de cada uno de ellos, llamado marca de clase, que normalmente es el punto medio del intervalo.
El segundo paso es colocar los datos en tablas que indiquen el número de veces que se repite cada modalidad, estas tablas se llaman tablas de frecuencias.
Frecuencia absoluta y frecuencia relativa
Ahora bien no es lo mismo que una modalidad se repita 5 veces en un total de 50 datos que en un total de 500. Por tanto, hablaremos de frecuencias absoluta y relativa.
Importante
-
La frecuencia absoluta es el número de veces que se repite una modalidad de una variable en un estudio estadístico. Se suele representar por
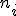. En el caso de que las modalidades sean intervalos tomamos como frecuencia absoluta de cada modalidad el número de observaciones agrupadas en el intervalo correspondiente.
-
La frecuencia relativa es el cociente entre la frecuencia absoluta
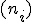y el número total de datos 
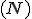. Se representa por 
.
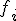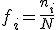
La suma de todas las frecuencias absolutas es igual al número total de datos .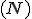
Y por tanto, la suma de todas las frecuencias relativas es 1.
Por último, añadir que multiplicando las frecuencias relativas por 100, obtenemos el tanto por ciento de esa modalidad en la muestra.
Frecuencias acumuladas
En multitud de ocasiones nos interesa agrupar los datos, de manera que, sin perder información, nos sean más útiles.
Por ejemplo, es interesante conocer en cuántas provincias se puede dormir en verano, es decir, cuántas están por debajo del umbral del sueño.
Tomando los siguientes datos, que se refieren a las temperaturas de una sola noche, obtenemos la tabla:
| Temperaturas |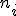
|
|
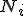
| 15ºC | 1 | 1 |
| 16ºC | 3 | 4 |
| 17ºC | 4 | 8 |
| 18ºC | 2 |
10 |
| 19ºC | 3 |
13 |
| 20ºC | 1 | 14 |
| 21ºC | 5 | 19 |
| 22ºC | 6 | 25 |
| 23ºC | 2 | 27 |
| 24ºC | 2 | 29 |
Sabiendo que para poder conciliar el sueño necesitamos una temperatura inferior a 22ºC, de la tabla anterior se deduce que solo en 19 de las provincias estudiadas han dormido a pierna suelta.
La tercera columna de la tabla hace referencia al concepto de frecuencia absoluta acumulada.
Actividad
La frecuencia absoluta acumulada es el resultado de sumar la frecuencia absoluta de una modalidad de la variable con todas las frecuencias de las modalidades anteriores.
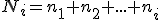
En consecuencia, las frecuencias relativas acumuladas representan la proporción de individuos de una muestra que presentan alguna de las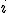 
primeras modalidades.
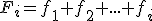
La última frecuencia absoluta acumulada es igual al número total de datos.
Y por tanto, la última frecuencia relativa acumulada es igual a 1.
Caso de estudio
En una biblioteca se ha realizado una encuesta entre los usuarios sobre los libros que se han leído en el último mes:
4,1,3,10,5,2,2,5,1,19,8,3,5,15,2,1,1,1,6,3,2,12,3,7,6,3,4,1,10,7,11,6,7,12,4,2,8,
5,9,3,6,8,2,1,12,9,8,5,2,3,3,4,3,7,9,1,4,9,5,8,6,12,17,3,9,6,7,5,5,3,9,7,8,11,2.
Caso de estudio
 |
Curso 2010/2011
En la corrección de errores tipográficos de un texto se han encontrado 22 páginas con un solo error en cada una, 9 páginas con 2 errores en cada una, 6 páginas con 3 errores en cada una, 3 páginas con 4 errores en cada una, 2 páginas con 5 errores en cada una y ningún error en las 58 páginas restantes.
Construya las tablas de frecuencias absolutas y relativas de la distribución del número de errores por página de ese texto.