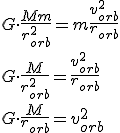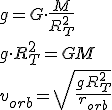3. Velocidad orbital y período de revolución
La determinación de la velocidad de un satélite en órbita es relativamente simple. Para ello basta aplicar la 2ª ley de Newton. Como tenemos una única fuerza y esta apunta siempre hacia el centro de la Tierra, no hay nada más que aceleración normal.
es el radio de la órbita (la distancia desde el centro del planeta sobre el cual se orbita).
La fuerza viene determinada por la ley de la Gravitación Universal:
Sustituyendo el valor de la fuerza de II en la primera expresión I tenemos:
Despejando se obtiene que:
Como puede deducirse a la luz de la expresión anterior, la velocidad orbital no depende de la masa del satélite.
Si es la Tierra el elemento masivo, la velocidad se puede expresar en función del campo gravitatorio en la superficie terrestre, g.
Como el movimiento de los astros lo suponemos circular por simplicidad de cálculo, podemos determinar ciertas magnitudes propias de este tipo de movimiento. Vamos a ver el caso del período. Recuerda: período es el tiempo que tarda en darse una vuelta completa. Se mide por tanto en segundos en el Sistema Internacional.
Para el caso que nos atañe, el movimiento planetario, se habla de período de revolución, y es el tiempo que tarda un satélite en recorrer una órbita completa y se calcula de la forma siguiente:
Para el caso del planeta Tierra
Importante
La velocidad en órbita de un satélite que describe un movimiento circular y uniforme alrededor de un planeta depende de la masa M del planeta y del radio de la órbita según la siguiente expresión:
![]()
Caso práctico
 |
| Imagen de NASAvia Wikimedia Commons. CC0 |
Imagina que el satélite de la fotografía, enviado por la NASA al espacio, tiene una masa de 180 kg y describe una órbita circular alrededor de la Tierra justo por su ecuador.
Calcula la velocidad de su órbita y su período de revolución si el radio de la misma es dos veces y media el radio terrestre. Datos: g = 9,8 m/s2; RT = 6,4·106 m