5. Lentes delgadas

Fíjate en esta secuencia de imágenes:

Imagen en Wikimedia de Frank C. Müller bajo licencia CC	Imagen en Wikimedia de Arbeiterreserve bajo dominio público	Imagen en Wikimedia de Julo bajo dominio público	Imagen en Wikimedia de Jgaguilar16 bajo licencia CC	Imagen en Wikimedia de Mavavf bajo licencia CC

La serie de objetos son de uso más o menos cotidiano, con un factor común. Todas presentan un sistema óptico formado por lentes. ¿Y qué es eso?

Pues, aunque, es posible que lo tengas muy claro en tu cabeza lo que es una lente, ya conoces la manía de los físicos de definir las cosas (¡qué pesados!). Bien, pues una lente es cualquier elemento transparente, homogéneo e isótropo, limitado por dos superficies de la cuales, al menos, una es curva. Su función es hacer que la luz converga o diverga, según interese y, aunque hay lentes de muchos tipos, todas ellas basan su funcionamiento en las leyes de la refracción que ya conoces.

Además ya verás que la desviación de los rayos también somos capaces de calcularla con la única condición de que las lentes sean delgadas. Esto significa suponer que las distancias desde el vértice y desde el centro de la lente son las mismas.

En la figura siguiente puedes ver los tipos de lentes más frecuentes. Las dos imágenes de la izquierda corresponden a lentes convergentes y las de la derecha a lentes divergentes.

Imagen en Wikimedia Commons de Jfmelero bajo licencia de GNU

Como ocurría con los espejos, las lentes forman una imagen de los objetos de los cuales les llega la luz. Podemos conocer dónde se encuentra esa imagen utilizando la llamada ecuación fundamental de las lentes delgadas:

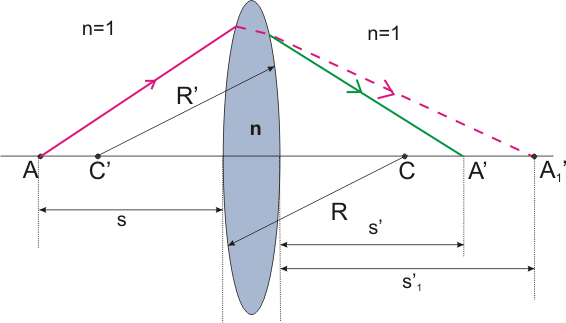
En esta expresión hemos tenido en cuenta que la lente tiene un índice de refracción n y que está situada en el aire. La imagen siguiente te ayudará a comprender mejor esta fórmula.

Imagen en Wikimedia Commons de Juancarcole bajo licencia CC

Como has visto, te hemos ahorrado la demostración de esta fórmula. Si estás interesado en ella te la dejamos más adelante en forma de ejercicio resuelto.

Por otra parte, de la ecuación fundamental podemos calcular la distancia focal f'. Para ello hacemos s=∞. en ese caso s'=f' y obtenemos la que se llama fórmula del constructor de lentes: