6. Análisis combinatorio
_of_combinatorial_species.svg.png "Combinación") |
| Imagen en Wikimedia Commons. Licencia CC |
Al hallar probabilidades de sucesos complicados, suele resultar difícil y tediosa una enumeración de los casos. La aplicación de la combinatoria facilita mucho esa tarea.
Importante
Principio fundamental del análisis combinatorio (principio de multiplicación)
Si un suceso puede ocurrir de 
formas, y si cuando éste ha ocurrido otro suceso puede ocurrir de 
formas, entonces el número de formas en que ambos pueden ocurrir en el orden especificado es 
formas.
El principio fundamental se puede generalizar para más de dos sucesos, como vamos a ver en el siguiente caso práctico.
Caso práctico
|
¿Cuántos grupos de seis cartas se pueden formar con una baraja de 40 cartas, en los siguientes casos? 1. Se extrae una carta y se devuelve a la baraja, así sucesivamente hasta extraer las seis cartas. 2. Se extrae una carta y no se devuelve a la baraja, esta acción se realiza de forma sucesiva hasta obtener el grupo de seis cartas. |
|
Un concepto importante dentro del estudio de la combinatoria es el de factorial, el cual vamos a ver a continuación.
Importante
Sea n un número entero no negativo, se define el factorial de n, n! de la siguiente forma:
- 0!=1
- Si n>0, entonces
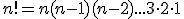
Del punto 2 se deduce que n!=n(n-1)!
Así por ejemplo, el factorial de los siguientes números es:
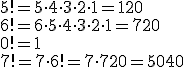
En ocasiones los sucesos que conforman un grupo de los mismos se ordena según una ley dada. Las principales formas de ordenación que se estudian en análisis combinatorio las vamos a ver a continuación.