Resumen

• Decimos que la media se corresponde con la idea de repartir todo lo que hay en partes iguales para todos.

La media es el promedio aritmético de las observaciones, es decir, el cociente entre la suma de todos los datos y el número total de ellos. Se representa por. Se calcula:

Sólo tiene sentido en variables cuantitativas, pues las x_i no son números en las variables cualitativas.

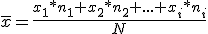
• Si ordenamos los datos de menor a mayor, la mediana, es el valor que está en medio, es decir, tiene tantos valores a la izquierda como a la derecha. Se representa por M_e.

Esta medida tiene sentido calcularla para cualquier tipo de variable cuantitativa. Destacar que cuando los datos se agrupan en intervalos se calcula el intervalo mediano.

El intervalo mediano es aquel que verifica que la frecuencia absoluta acumulada en su extremo inferior (N_i-1) es menor que N/2 y la frecuencia absoluta acumulada en su extremo superior (N_i) es mayor que N/2. De manera equivalente el intervalo mediano verifica que N_i-1/N < 1/2 y N_i/N>1/2.

• Decimos que la moda es el valor que más se repite, es decir el de mayor frecuencia absoluta. Se representa por M_o.

Esta medida tiene sentido calcularla para cualquier tipo de variable.

Claramente cuando la variable es cuantitativa continua no tiene sentido hablar de valor más frecuente, si no, de intervalo modal.

En caso de que varias modalidades tengan la frecuencia máxima, se habla de distribución multimoda (con 2 o más modas).

 

Las medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central.

 

Los más importantes son el recorrido, la varianza, la desviación típica y el coeficiente de variación.

• El recorrido de una variable es la diferencia entre el mayor y menor valor que toma esa variable. Se representa por R.

• La varianza mide la dispersión de una muestra en función de la diferencia (la distancia) de cada uno de los elementos de la muestra con el valor medio de la misma. Se representa por s².

Se calcula mediante la fórmula:

• La desviación típica es la raíz cuadrada positiva de la varianza. Se representa por σ=.

Aunque tanto la varianza como la desviación típica son medidas de la variación con respecto a la media y tienen un significado semejante, la desviación típica se utiliza con más frecuencia porque se expresa en las mismas unidades que los valores de las variables. Al contrario que la varianza, cuyos valores se expresan en unidades al cuadrado.