2.1 Definición y propiedades
Ejemplo:
Vamos a coger una de las funciones del punto anterior, por ejemplo, la función f(x) = 2x.
Cógete la calculadora y construye una tabla de valores para la función. Por ejemplo, algo similar a ésta:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x)=2x |
0,125 | 0,25 | 0,5 | 1 | 2 | 4 | 8 |
Imagínate ahora una función que fuera al revés, es decir, una función que del resultado fuera al valor de partida, por ejemplo, cuando yo le diera el valor 8, ella me diera como resultado 3. Vamos a llamar g(x) a esa función. Así la tabla de valores para g sería la contraria:
| x | 0,125 | 0,25 | 0,5 | 1 | 2 | 4 | 8 |
| g(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Pues bien, esa función g(x) que hemos construido, sería la función inversa de la función inicial f(x) = 2x.
Observa la siguiente escena de Geogebra. Puedes modificar la base de la función exponencial y de su inversa ( o recíproca) manipulando el deslizador. Fíjate también en que los puntos de la inversa se obtienen intercambiando sus coordenadas:
Como puedes ver, pongas la base que pongas, las dos funciones son simétricas respecto a la bisectriz del primer cuadrante, propiedad que cumplen todas las parejas de funciones inversas.
La expresión analítica de la función g es:
![]()
Y es que, así es como vamos a llamar a esa función inversa (o recíproca), LOGARITMO.
Reflexiona
Contesta a las siguientes cuestiones a partir de la escena anterior:
- ¿Para qué valores de la base "a" existe la función logaritmo?
- ¿Cuál es el dominio de la función logaritmo?¿Y el recorrido?
- ¿Por qué punto pasa siempre?
- Según el valor de "a", ¿cómo es la función, creciente o decreciente?
- ¿Hay alguna asíntota?
Importante
La función logaritmo en base a de x, se define como la función inversa de la función exponencial y= ax, y se expresa:
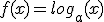 con a>0 y distinto de 1
con a>0 y distinto de 1
Propiedades de la función logaritmo:
- El dominio es R+; el recorrido es R
- Es continua en todo el dominio
- Si a>1 la función es creciente en todo su dominio
- Si 0<a<1 la función es decreciente
- Corta al eje OY en el punto (1,0)
- El eje OY es una asíntota vertical
Pero no es necesario recurrir a la función inversa para poder describir o formar la función logaritmo.
El logaritmo, por sí solo es una operación matemática, y para calcularlo, hay que hallar el número que al elevar la base por él, me dé el argumento del logaritmo. Puedes repasar las propiedades relacionadas con los logaritmos en el siguiente vídeo:
Vídeo de estudiia alojado en Youtube
Ejercicio Resuelto
Ahora que ya sabemos calcular cualquier logaritmo, sí que podemos hacer la gráfica de una función logaritmo, sabiendo cómo ha de ser la forma, basta con calcular una tabla de valores para ajustar el gráfico.
Por ejemplo, vamos a representar gráficamente, la función 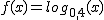 .
.
Comprueba lo aprendido
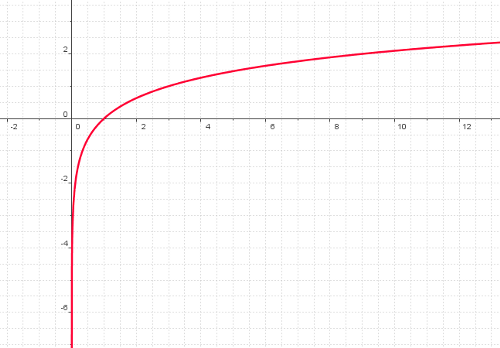
Ahora te toca a ti. Coge lápiz, papel y calculadora y siguiendo el mismo procedimiento representa gráficamente la función:
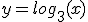
Debe salirte una gráfica similar a esta:
Importante
En un logaritmo, el argumento, es decir, el número sobre el que opera siempre tiene que ser positivo.
Así, si en lugar de loga (x), tenemos la función f(x) = loga (g(x)), el dominio será el conjunto de puntos donde g(x) es positivo;
Dom(f) = {x / g(x)>0 }
Es decir, cuando el argumento del logaritmo es distinto de la función x, tenemos que estudiar cuándo es mayor que 0.
Ejemplo:
Veamos un ejemplo concreto en el siguiente vídeo:
Vídeo de lasmatematicas.es alojado en Youtube
Para saber más
Traslaciones de la función logaritmo
En la siguiente escena puedes ver qué ocurre si multiplicamos la función logaritmo por una constante o se la sumamos:
Curiosidad
Logaritmo y pH
En la Naturaleza se dan situaciones en las que se tienen que utilizar medidas de órdenes muy diferentes. Por ejemplo, si hablamos del peso de los seres vivos, tenemos que:
- Un hombre puede pesar 90 kg = 90.000 gr = 10 4,96 gr
- Un rotífero (el menor animal pluricelular): 0,00000000603 gr = 10 –8,22 gr
- Una ballena (el mayor de todos los animales): 120 T = 120.000.000 gr = 10 8,08 gr
Así que si tenemos que referirnos a diferentes animales por sus pesos o hacer una gráfica con los mismos, es un gran inconveniente que haya tan enormes diferencias entre unos y otros. Una solución para abreviar la expresión de esas diferencias es asignar a cada animal el logaritmo decimal de su peso.
Así, al hombre le asignaríamos el valor 4,96, al rotífero -8,22 o a la ballena 8,08, cifras en cualquier caso mucho más cómodas de manejar. En este caso, estaríamos usando una escala logarítmica que iría aproximadamente desde -8 hasta 8.
Pues bien algo muy similar se utiliza para asignar la medida del pH de una determinada solución. Seguro que has visto y oído más de una vez eso de "pH neutro" en algún producto de aseo como champú, gel, desodorante,...
El pH es la concentración de iones hidronio [H3O+] presentes en determinada sustancia. La sigla significa "potencial de hidrógeno". Este término fue acuñado por el químico danés Sørensen, quien lo definió como el logaritmo negativo de base 10 de la actividad de los iones hidrógeno. Esto es:
![\mbox{pH} = -\log_{10} \left[ \mbox{a}_{H_3O^+} \right]](http://upload.wikimedia.org/math/7/b/7/7b7e772992e9d43888cd421cba60c766.png)

Desde entonces, el término "pH" se ha utilizado universalmente por lo práctico que resulta para evitar el manejo de cifras largas y complejas.
La escala logarítmica del pH va de 0 a 14 en disolución acuosa, siendo ácidas las disoluciones con pH menores a 7, y básicas las que tienen pH mayores a 7. El pH = 7 indica la neutralidad de la disolución (donde el disolvente es agua).
Por ejemplo, los jugos gástricos tienen pH= 1,5, el vinagre 2,9, la leche 6,5, el agua 7, el jabón entre 9 y 10 y el amoniaco 11,5.