1. Estadística descriptiva unidimensional

SÍNTESIS.

Estadística Descriptiva. La estadística se puede dividir en dos partes:
* Estadística descriptiva o deductiva.
* Estadística inferencial o inductiva.
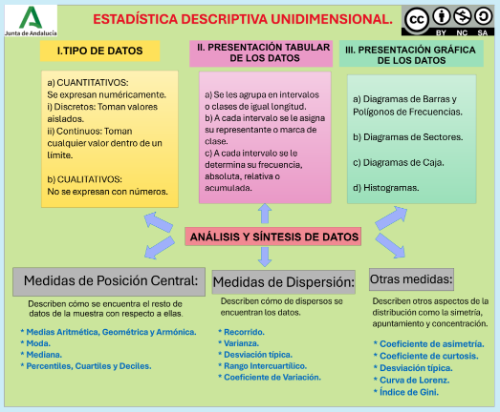
En esta ocasión nos hemos ocupado de la estadística descriptiva o deductiva que trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones. Se construyen tablas y se representan gráficos que permiten simplificar en gran medida, la complejidad de todos los datos que intervienen en la distribución. Asimismo se calculan parámetros estadísticos que caracterizan la distribución. En esta parte de la estadística no hemos hecho uso del cálculo de probabilidades, y únicamente nos hemos limitado a realizar deducciones a partir de los datos y parámetros obtenidos. El objetivo básico de la Estadística es extraer la información contenida en un conjunto de observaciones. Resumir los datos es un procedimiento útil para conseguirlo y puede hacerse mediante tablas, gráficos o valores numéricos. A lo largo de esta situación hemos visto las principales técnicas numéricas y gráficas para describir una característica de interés observada en una población, poniendo en relieve sus rasgos más importantes. Hemos también usado distintos recursos tecnológicos como la Hoja de Cálculo, Calculadora y GeoGebra para ayudarnos en esta labor.

Esquema de los contenidos de la situación de aprendizaje. — Material de elaboración propia. *Estadística descriptiva unidimensional.* (CC BY-NC-SA)

2. Las fórmulas del éxito

1.- La Media. $\bar {x}$.

Se define de la siguiente manera: $\bar {x}={\large{\frac{\sum _{i=1}^k x_i·n_i}{\sum _{i=1}^k n_i}}}={\large{\frac{\sum _{i=1}^k x_i·n_i}{n}}}$.

2.- La Mediana. $M_e$.

Para su cálculo, y suponiendo que los valores están agrupados, se procederá de la siguiente manera:
$M_e=l_{i-1}+{\large{\frac{n/2-N_{i-1}}{n_i}}}·a_i$, donde $l_{i-1}$ es el límite inferior del intervalo donde se encuentra la mediana y $a_i$ es su amplitud.

3.- La Moda. $M_o$.

Suponiendo que los valores están agrupados, se procederá de la siguiente manera:
$M_o=l_{i-1}+{\large{\frac{n_i-n_{i-1}}{(n_i-n_{i-1})+(n_i-n_{i+1})}}}·a_i$

4.- La Varianza, $\sigma^2_x$ y la Desviación Típica, $\sigma_x$.

La varianza viene dada por la expresión $\sigma^2_x={\large{\frac{\sum _{i=1}^k (x_i-\bar {x})^2·n_i}{n}}}$. A efectos de su cálculo, es preferible esta otra expresión, $\sigma^2_x={\large{\frac{\sum _{i=1}^k x^2_i}{n}}}-\bar {x}^2$. Como la desviación típica es la raíz cuadrada positiva de la varianza, aquélla vendrá dada en las mismas unidades que la variable.

5.- Recorrido intercuartilítico

$R_I=Q_3-Q_1$.

6.- Coeficiente de Variación (Pearson)

$CV={\Large{\frac{\sigma_x}{\bar{x}}}}$.

7.- Simetría

Nos podemos encontrar con dos casos:

Si la distribución tiene forma de campana se utiliza la expresión $A_s={\large{\frac{\bar{x}-M_o}{\sigma_x}}}$ (Primer Coeficiente de Pearson).
Si la distribución no tiene forma de campana o se desconoce este hecho, se calcula la simetría por la expresión $g_1={\Large{\frac{m_3}{\sigma^3_x}}}$ (Coeficiente de Asimetría de Fisher).