2.1. Teorema del seno
Un triángulo oblicuángulo es un triángulo no rectángulo. Utilizaremos la expresión resolver un triángulo cuando queramos conocer todos sus elementos, es decir, la longitud de sus tres lados y la medida de sus tres ángulos.
Para esta resolución utilizaremos las siguientes propiedades: la suma de los tres ángulos del triángulo, el teorema del seno y el teorema del coseno.
Importante
En cualquier triángulo de ángulos A, B y C, y lados a, b, c, se cumple que
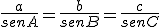
En la siguiente escena, mueve los vértices del triángulo, y así podrás comprobar cómo se cumple el teorema anterior.
Comprueba lo aprendido
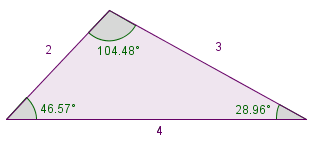
Vamos a completar las siguientes afirmaciones sobre este triángulo:
Importante
El teorema del seno permite determinar la longitud de uno de los lados de un triángulo, conociendo:
- El ángulo opuesto al lado que queremos calcular
- Otro lado
- El ángulo opuesto a este lado
Reflexiona
Para resolver un triángulo donde conocemos un lado, a, y sus dos ángulos adyacentes B y C, debemos calcular los lados b y c, y el ángulo A.
En este caso la única limitación es que la suma de los dos ángulos no puede ser superior a 180º (para que pueda ser un triángulo).
Importante
Para calcular el ángulo que nos falta, utilizamos la propiedad que nos relaciona los tres ángulos de un triángulo. En cuanto a los lados, debemos utilizar el teorema del seno, ya que nos relaciona los dos lados de un triángulo con los dos ángulos opuestos correspondientes.
| SUMA DE LOS ÁNGULOS | TEOREMA DEL SENO | TEOREMA DEL SENO |
|
|
|
|
Reflexiona
Caso de estudio
Ayudemos al pobre Sinuhé a resolver este problema.
Si la longitud del barco es 30 metros y las cuerdas tienen una inclinación de 45º y 30º con respecto a la cubierta del barco, ¿cuál es la longitud de las cuerdas?