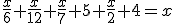2.3. Resolución de problemas
En el tema 2 del bloque 1 había un apartado dedicado a la resolución de problemas aritméticos, del que destacaba la siguiente presentación:
Todos estos conceptos y técnicas son aplicables a los problemas algebraicos y de resolución de ecuaciones, pero se le añade una dificultad más: la detección de la incógnita y el planteamiento del problema desde un punto de vista algebraico.
El siguiente esquema resume los 4 pasos que hay que seguir para llegar a la solución de un problema de este tipo:
Imagen de elaboración propia
Como ocurría en los problemas aritméticos, no hay una fórmula mágica para resolver estos problemas pero lo que sin duda nos ayuda es la práctica. Por eso, te proponemos una lista de reproducción con 2 vídeos del canal de Youtube lasmatematicas.es:
Ejercicio Resuelto
Resuelve los problemas anteriores, siguiendo los pasos que se indican en la imagen de arriba:
Problema 1
La madre de Jorge tiene 39 años y dice que tiene 6 años menos que el triple de la edad de su hijo. ¿Qué edad tiene Jorge?
Problema 2
¿Cuál es el número que aumentado en 55 es igual a 6 veces su valor inicial?
Curiosidad
Aunque ya vimos que la notación que usamos hoy en día para escribir en lenguaje matemático es relativamente actual, las ecuaciones se han resuelto desde la civilización egipcia.
En el Papiro de Rhind (1650 a.C.) se resuelven problemas de un modo análogo al que se usa hoy en día. Uno de los problemas que aparece en este documento es "Un montón y un séptimo del mismo es igual a 24"
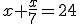
Los babilonios, unos 1000 años después, se centraron básicamente en las ecuaciones de segundo grado; y entre los griegos, que en general se dedicaron a la geometría, debemos destacar la figura de Diofanto de Alejandría (200 a.C. - 284 a.C.). Diofanto publicó en su obra sus estudios acerca de ecuaciones que tienen soluciones racionales. Como curiosidad, has de saber que su epitafio era un problema que se resuelve con una ecuación de primer grado. Dice así:
"Transeúnte, ésta es la tumba de Diofanto: es él quien con esta sorprendente distribución te dice el número de años que vivió. Su niñez ocupó la sexta parte de su vida; después, durante la doceava parte su mejilla se cubrió con el primer bozo. Pasó aún una séptima parte de su vida antes de tomar esposa, y cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorándole, durante cuatro años. De todo esto se deduce su edad."
Este problema se traduce en la siguiente ecuación, siendo x la edad de Diofanto: