1.1. Expresiones algebraicas
¿Qué es el lenguaje algebraico?
Si recuerdas, en la unidad anterior estudiamos las magnitudes, entre ellas la presión. En su momento dijimos que la presión era el cociente entre la fuerza y la superficie y dimos una fórmula para saber calcularla. Aunque en ese momento no lo supieses, estábamos haciendo uso de un lenguaje algebraico.
 |
| Imagen de brainware3000en Flickr. LicenciaCC |
Importante
El lenguaje numérico expresa la información matemática a través de los números. Sin embargo, en algunas ocasiones es necesario utilizar letras para expresar números desconocidos. El lenguaje algebraico expresa la información matemática mediante letras, números y símbolos.
Cuando pasamos del lenguaje ordinario al lenguaje algebraico ponemos de manifiesto los datos (que simbolizamos por letras), las operaciones que los ligan (a través de símbolos preestablecidos) y las relaciones entre los mismos (por ejemplo, la de igualdad).
Es costumbre en ciertos campos de las ciencias usar letras determinadas según el objeto con el que se esté trabajando. Así por ejemplo, si manejamos números naturales en sucesiones, es usual utilizar las letras m y n.
Otro ejemplo, en geometría se suelen utilizar letras mayúsculas para referirnos a los ángulos, puntos, superficies, volúmenes... mientras que se utilizan letras minúsculas para las medidas lineales (longitudes). En Física, en el estudio del movimiento el espacio se simboliza por e, la velocidad por v y el tiempo por t.
Aunque en teoría se podría utilizar cualquier letra para simbolizar las magnitudes anteriores, respetar el lenguaje preestablecido es síntoma de conocimiento y soltura.
Expresiones algebraicas
Precisamente el paso del lenguaje usual al lenguaje algebraico, da como resultado una expresión algebraica.
Importante
Una Expresión Algebraica es aquella en la que usamos números y letras relacionadas por operaciones matemáticas.
Cada expresión algebraica tiene un significado. De hecho, cuando tenemos un problema, intentamos traducirlo al lenguaje algebraico mediante una expresión. Cada uno de los valores (variables) que no conocemos lo representaremos por una letra diferente. Mira los siguientes ejemplos:
|
Enunciado |
A un número le sumamos 4 unidades | El doble de un número | La cuarta parte de un número, menos su cuadrado | El coste de 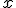 kg de naranjas, si valen a 1,80 €/kg kg de naranjas, si valen a 1,80 €/kg |
El 15% de un precio |
|
Expresión algebraica |
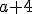 |
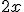 |
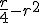 |
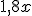 |
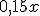 |
Comprueba lo aprendido
En el siguiente applet del Proyecto Ed@d puedes practicar el cambio de lenguaje usual a lenguaje algebraico:
Escena de Montserrat Doménech Tomasa en Proyecto Descartes. Licencia CC
Valor numérico de una expresión algebraica
Una expresión algebraica también nos puede servir para buscar generalizaciones de un problema.
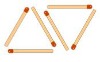
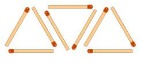
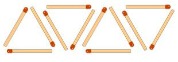
Imagina que construimos triángulos con cerillas del siguiente modo:
|
Nº de triángulos (n) |
1 |
2 |
3 |
4 |
 |
 |
 |
 |
|
|
Nº de cerillas (p) |
3 |
6 |
9 |
12 |
¿Podríamos averiguar cuántas cerillas necesito si quiero formar 100 triángulos?
Para ello tenemos que encontrar una relación entre el número de triángulos (n) y el número de cerillas (p). Si te fijas, por cada triángulo necesito 3 cerillas, por lo que podríamos deducir que p=3n. Conociendo esta regla, ya puedo saber que para n=100 será p=3·100=300 cerillas.
Importante
Si en una expresión algebraica se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el valor númerico de la expresión algebraica para los valores de las letras dados.
Comprueba lo aprendido
Curiosidad
Si pinchas en la siguiente imagen descubrirás multitud de símbolos matemáticos, algunos ya conocidos y muchos otros por conocer. Con casi toda seguridad que en alguna ocasión (no muy lejana) tendrás que recurrir a esta fuente:
 |
| Imagen en www.3con14.com. Licencia CC |