1.2. Clasificación de los sistemas de ecuaciones lineales.
 |
Aunque hay gente que suele decir que todo tiene solución menos la muerte, lo cierto es que en la vida cotidiana hay veces que tenemos algunas restricciones en nuestros problemas que unas veces hacen que tengamos solución y otras veces no, incluso a veces tenemos varias soluciones posibles. Por ejemplo si queremos viajar de Cádiz a Madrid por carretera hay varias formas de hacerlo, ya que podemos ir en dirección a Córdoba y después recorrer la autovía de Andalucía o bien llegar a Sevilla y tomar dirección a Mérida y al llegar a ella tomar ya la dirección de Madrid.
Con los sistemas va a pasar algo parecido, habrá veces que tengan una única solución o varias.
Importante
Un sistema de ecuaciones lineales se dice que es Compatible si tiene solución y en caso contrario se llama Incompatible.
Si el sistema tiene una única solución recibe el nombre de Compatible Determinado. Si tiene infinitas soluciones se llama Compatible Indeterminado.
El problema se nos va a plantear para saber cuándo un sistema es de un tipo u otro. Por ejemplo, el sistema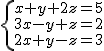 
tiene como única solución los valores (1, 2, 1), puedes comprobar que si intentas cualquier otro trio de valores para x, y, z siempre te va a dar que no es solución.
Sin embargo el sistema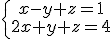 
no solo tiene por solución 
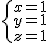, si no que cualquiera de las ternas (2, 1, -1) ó (-1, 2, 4) también son solución, y no son las únicas.
Vamos a ver cómo todo lo que hemos aprendido hasta el momento en la unidad tiene su aplicación.
Importante
El Teorema de Rouché o de Rouché-Frobenius nos dice que en un sistema de ecuaciones lineales el número de soluciones depende de los rangos que tengan la matriz ampliada y la de los coeficientes mediante la siguiente regla.
1) Si el rango de la matriz de los coeficientes es igual al rango de la matriz ampliada e igual al número de incógnitas, el sistema es Compatible Determinado.
2) Si el rango de la matriz de los coeficientes es igual al rango de la matriz ampliada pero menor que el número de incógnitas, el sistema es Compatible Indeterminado.
3) Si el rango de la matriz de los coeficientes es distinto del rango de la matriz ampliada, el sistema es incompatible.
En el siguiente video puedes ver ejemplos del estudio, mediante el teorema anterior, de distintos sistemas de ecuaciones.
Para que puedas practicar lo que has visto, en el siguiente enlace tienes un test en el que te hacen preguntas sobre la utilización del Teorema de Rouché para estudiar un sistema. Contesta a las preguntas para ver si has entendido lo que llevamos hasta el momento.
AV - Actividad de Espacios en Blanco
Tenemos tres sistemas, cada uno con una cantidad distinta de soluciones. Utiliza el Teorema de Roché para responder a las cuestiones:
