2.1 Trabajo mecánico

Como has visto en el apartado anterior, para que se produzca trabajo es necesario que exista una fuerza que provoque un desplazamiento a un sistema o parte del mismo.

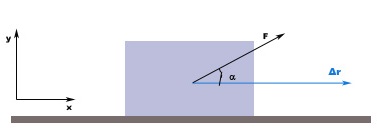
Por lo tanto, para definir matemáticamente el trabajo se necesita una fuerza F que actúe sobre un cuerpo produciendo un desplazamiento de su punto de aplicación Δr sobre una superficie horizontal, de forma que el desplazamiento sea rectilíneo. En el caso general de que la dirección de la fuerza forme un ángulo

respecto a la dirección de desplazamiento, el esquema de la situación será tal y como se representa en la siguiente figura:

Imagen de elaboración propia

Debido a que únicamente la componente de la fuerza que provoca movimiento realiza trabajo, en este caso la componente sobre el eje x, el trabajo mecánico realizado dependerá solo de ella y podremos enunciar la definición de trabajo mecánico:

Importante

Se denomina trabajo mecánico (W) realizado por una fuerza F que actúa sobre un cuerpo, al producto escalar del vector fuerza 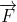$\overrightarrow{F}$ por el vector desplazamiento $\Delta \overrightarrow{r}$ experimentado.

W = \vec F\cdot\bigtriangleup \vec r = F\cdot\bigtriangleup r \cdot\cos \propto

La unidad de trabajo en el Sistema Internacional es el Julio (J), definida como el trabajo realizado por una fuerza de 1 N cuando su punto de aplicación se desplaza 1 m en la misma dirección y sentido que la propia fuerza (1 J = 1 N·m)

De la definición anterior puede deducirse que:

Cuando la fuerza aplicada tiene la misma dirección y sentido que el desplazamiento, esta ayudará al movimiento (acelera). Como el ángulo entre ambas es menor que 90º se cumple que cos 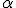> 0 y el trabajo es positivo (W > 0)
Si la fuerza aplicada tiene igual dirección pero sentido contrario al desplazamiento, esta se opone al movimiento (frena). Como el ángulo entre ambas es mayor que 90º se cumple que cos 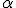< 0 y el trabajo es negativo (W < 0)
Cuando la fuerza es perpendicular al desplazamiento 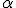= 90º, por lo que cos 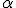= 0 y por tanto W = 0.

Por lo tanto, una fuerza perpendicular al movimiento no realiza trabajo.

Caso práctico

Imagen de elaboración propia

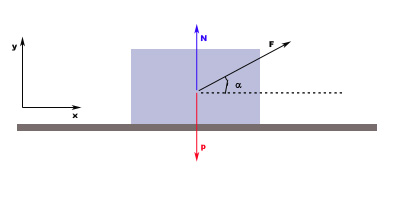
Sobre un objeto de masa 5 kg que está en reposo y situado en una superficie horizontal sin rozamiento se aplica una fuerza de 25 N que forma un ángulo de 30 grados respecto a la horizontal. Bajo la acción de esta fuerza el objeto se desplaza 10 m en la dirección de la fuerza.

El diagrama de fuerzas que actúan lo tienes representado en la imagen.

a) Determina el trabajo realizado por cada una de las fuerzas.

b) Si se cambia la superficie por otra de coeficiente dinámico de rozamiento μ_di = 0.3, ¿cuál será el trabajo realizado por cada una de las fuerzas? ¿Y el trabajo total realizado sobre el objeto?

Retroalimentación

En este caso, aparece una nueva fuerza en el conjunto: la fuerza de rozamiento F_R, de igual dirección que el movimiento pero de sentido contrario al mismo, tal y como se observa en la imagen.

Las fuerzas N, p y F son las mismas que en el apartado anterior, por lo que el trabajo realizado por cada una de ellas será el ya calculado:

W_N = W_p = 0 , W_F = 216.5 N

Sin embargo ahora existe la fuerza de rozamiento F_R que realiza un trabajo no nulo que hay que calcular. Para ello, será necesario en primer lugar calcular su módulo, para lo que deberás hacer uso de lo que has aprendido en dinámica, descomponiendo las fuerzas en sus ejes:

Eje y: N + Fy - p = 0 → N = p - 25·sen 30= m·g = 5·9.8 = 36.5 N

Esto permite calcular F_R = µ·N = 0.3·36.5 = 10.95 N

Toda fuerza de rozamiento siempre se opone al movimiento, por lo que su ángulo es de 180º, con lo que el trabajo resulta: W_FR = 14.7·10·cos 180º = -109.5 J

Observa que el resultado es negativo, como cabía esperar de una fuerza que "frena" al sistema.

El trabajo total realizado sobre el objeto resulta:

W_T= W_N+W_p+ W_F+ W_FR =0 + 0 +216.5 - 109.5 = 107 J

Importante

Cuando sobre un cuerpo actúa más de una fuerza de forma simultánea, el trabajo realizado por la fuerza resultante, suma vectorial de todas ellas, es igual a la suma de los trabajos realizados por cada una de ellas por separado.

Ejercicio Resuelto

Comprueba la afirmación anterior con los datos del apartado b) del ejercicio anterior.

Reflexiona

Imagina que quieres desplazar 2 metros un objeto tirando de él y realizando la mínima fuerza posible. Con qué ángulo lo harías?

Retroalimentación

El trabajo necesario para desplazar un objeto una determinada distancia es siempre el mismo, no así la fuerza necesaria para hacerlo. Si observas la expresión del trabajo W = F·Δr·cos α , como la distancia es constante (2 m), el producto F·cos α también lo será, y para hacer mínima F tendremos que maximizar cos α.

El coseno es una función periódica cuyo valor máximo es 1, valor que toma cuando α = 0º. Como el ángulo en el cálculo del trabajo es el formado con la dirección de desplazamiento, un ángulo de cero grados corresponde a la aplicación de la fuerza en la misma dirección del desplazamiento.

Aplicar una fuerza en cualquier otra dirección implicaría que parte de ella (la componente en la dirección perpendicular) no sería útil, al no realizar trabajo.