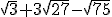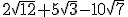5. Operaciones con radicales
La propiedad principal de las raíces es 
. Por tanto, una raíz se puede transformar en una potencia, luego las propiedades que verifican las raíces son básicamente equivalentes a las de las potencias.
Importante
Las principales propiedades que verifican las raíces son las que se indican en la siguiente tabla, y se deducen al aplicar las propiedades de las potencias:
|
Producto de raíces del mismo índice |
|
|
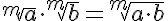
Cociente de raíces del mismo índice |
|
|
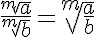
Raíz de otra raíz |
|
|
Raíz de una potencia |
 |
|
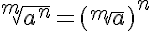Simplificación |
|
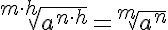
De la propiedad de simplificación se deduce otra propiedad que aplicamos continuamente: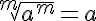 
Extracción e introducción de factores en radicales.
Para sacar factores de una raíz, se debe descomponer el radicando en factores primos, de manera que las potencias de la descomposición cuyo exponente sea el índice o un múltiplo del índice de la raíz podrán salir fuera de la raíz, que quedará simplificada.
Ejemplos: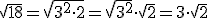 
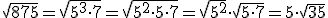
En ocasiones puede resultar útil introducir factores de la raíz, haciendo un proceso inverso:
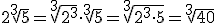
Suma y resta de radicales.
Para poder sumar o restar raíces tienen que tener el mismo radicando, de forma que la sumas y restas se realizan sacando factor común de la raíz que se repite.
Ejemplo: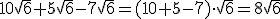 
Tienes que tener muy claro que 
. Cuando haya suma o resta de raíces con distinto radicando, NO se puede realizar la operación y se deja expresada la suma tal cual.
Ejemplo o ejercicio resuelto
Opera y simplifica:
Producto y cociente de radicales.
Para poder multiplicar o dividir raíces tienen que tener el mismo índice. Un paso previo será por tanto pasar las raíces a un índice común, calculando el mínimo común múltiplo de los índices y utilizando la propiedad de simplificación.
Cuando dos raíces tienen el mismo índice, es menor la que tiene menor radicando. Por ejemplo,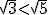 
.
Ejemplo o ejercicio resuelto
- Pasa a radicales con índice común las raíces
.
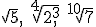- Pasa a radicales con índice común, y ordena de menor a mayor, las raíces
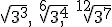
- Calcula
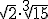
- Calcula
|
|
|
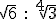
