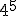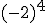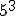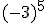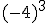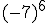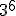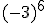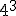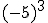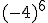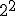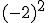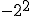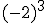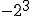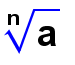4. Potencias y raíces
 Fotografía en Flickr de Sifu Renka bajo CC
|
Igual que el producto de números naturales es una manera abreviada de representar la suma repetida de un número, elevar un número a una potencia natural expresa el producto repetido de un número por sí mismo.
Por ejemplo, si un restaurante nos ofrece un menú compuesto por un primer plato, segundo plato y postre, disponiendo de cuatro posibilidades para cada uno de ellos, ¿cuántos menús distintos se podrían pedir?
Habría 4 posibilidades para el primero. Para cada una de esas posibilidades se dispondrían de otras cuatro para el segundo, o sea, 4 posibilidades para la opción 1, 4 para la opción 2, etc. Esto nos arroja que por el momento tenemos 4·4=16 posibilidades, y para cada una de ellas un postre distinto, o sea, 16 con el postre 1, 16 con el postre 2, etc. Así tenemos 16·4=64 posibilidades. O mejor dicho, 4·4·4 posibilidades. Esto lo podemos expresar así: 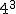
Actividad
Dado un número a y un número natural n, llamamos potencia de base a y exponente n, al número
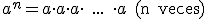
que se consigue multiplicando la base a, por sí misma tantas veces como indique el exponente n. Por ejemplo:
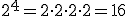 ;
; 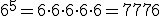 ;
; 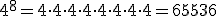
La potencia x2 se llama cuadrado, y la potencia x3 cubo. Las siguientes se llaman potencia cuarta, quinta, sexta, ... y, en general, xn se llama enésima potencia o n-ésima potencia.
Caso de estudio
Ejercicio
Utilizando la definición anterior, y tu calculadora científica resuelve las siguiente potencias:
Una vez realizadas las potencias, pincha en Ver solución para comprobarlas.
Ahora te toca a ti:
Intenta calcular las siguientes potencias que, aunque parecen iguales, hay algunas diferencias:
Actividad
Si observas detenidamente el ejemplo anterior podemos sacar algunas conclusiones:
- Si el signo está dentro del paréntesis, formará parte de la base y por consiguiente se repetirá tantas veces como nos indica el exponente.
- Si el signo está fuera del paréntesis, no forma parte de la base y por consiguiente se añadirá al resultado de la potencia.
- Si la base es positiva, el resultado será positivo.
- Si la base es negativa y el exponente es par, el resultado será positivo.
- Si la base es negativa y el exponente es impar, el resultado será negativo.
Las raíces o radicales.
Asociado al concepto de potencia tenemos su operación contraria que es la extracción de raíces, es decir, dado un número, nos planteamos qué otro número elevado a cierta potencia da el número inicial. Por ejemplo, si tienes un cuadrado cuyo lado mide un metro, aplicando el teorema de Pitágoras se obtiene que la diagonal del cuadrado mide un número que al elevarlo al cuadrado de dos, que lo representamos como  .
.
Las raíces también son necesarias, por ejemplo, para hallar la arista de un cubo cuyo volumen sea 7 cm3. Para ello basta resolver la ecuación x3 = 7, obteniéndose una raíz cúbica: 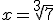 , es decir, se trata de un número que al elevarlo al cubo nos de siete.
, es decir, se trata de un número que al elevarlo al cubo nos de siete.
Importante
La radicación u obtención de raíces es la operación contraria a elevar un número a una potencia. Se expresan con el símbolo radical:
El valor que aparece dentro del símbolo radical se llama radicando, y la cantidad que aparece encima del radical se llama índice de la ráiz. Esta expresión nos indica el número que al elevarlo a n nos de el número a, es decir: 
Cuando en un radical no se expresa el índice, por convenio se establece que se está calculando una raíz cuadrada, es decir, por ejemplo, se escribe 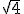 en lugar de
en lugar de 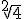 .
.
Empezarás a trabajar con radicales a partir del punto 4.3, pero antes debes conocer unas propiedades o características básicas que poseen las raíces.
En primer lugar, debes observar que las raíces de índice par de un número positivo no son únicas; si quieres obtener la raíz cuadrada de 25, es decir, un número que multiplicado por sí mismo sea igual a 25, es claro que +5 resuelve el problema, pero también -5.
Ejemplo: 
Y en segundo lugar, observa que si el radicando es negativo, sólo se pueden calcular raíces que sean de índice impar.
Ejemplo:  ya que (-5)·(-5)·(-5) = -125. Y sin embargo no se puede obtener
ya que (-5)·(-5)·(-5) = -125. Y sin embargo no se puede obtener 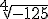 o la
o la 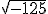 .
.
En efecto, está claro que 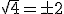 ya que 2·2 = +4 y (-2)·(-2) = +4, pero piensa en
ya que 2·2 = +4 y (-2)·(-2) = +4, pero piensa en 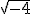 , ¿puede haber algún número que al multiplicarlo por sí mismo de -4? No, no es posible, ya que por la regla de los signos, un número positivo por otro positivo da positivo, e igualmente un número negativo por otro negativo da un resultado positivo, luego al multiplicar un número un número par de veces, siempre saldrá una cantidad positiva, nunca negativa.
, ¿puede haber algún número que al multiplicarlo por sí mismo de -4? No, no es posible, ya que por la regla de los signos, un número positivo por otro positivo da positivo, e igualmente un número negativo por otro negativo da un resultado positivo, luego al multiplicar un número un número par de veces, siempre saldrá una cantidad positiva, nunca negativa.