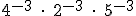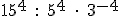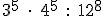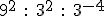4.3. Potencias de exponente fraccionario
| fuente propia |
Tras estudiar las potencias de exponente natural y exponente entero, vamos a analizar las potencias de exponente fraccionario. Para entender mejor cómo es una potencia de exponente fraccionario, vamos a hacer algunos ejercicios.
Vas a necesitar la calculadora científica no solo para calcular potencias, en la cuales deberás poner entre paréntesis las potencias fraccionarias, sino también para calcular raíces de índice distinto de 2.
En tu calculadora debes localizar la tecla INV O SHIFT,que sirve para utilizar las funciones matemáticas que vienen encima de cada tecla de la calculadora. Pues bien, la manera de poder utilizar esas funciones es dar a esa tecla que está arriba a la izquierda, y que según la calculadora se llama "INV" o "SHIFT".
|
|
|
| fuente propia bajo CC |
|
Para escribir raíces y potencias, tenemos varias teclas que son las siguientes:
|
fuente propia bajo CC |
La primera como se ve es para la raíz cuadrada: pulsamos esta tecla, después la cantidad y la calculadora nos da la solución. La segunda es para elevar al cuadrado un número y la tercera es para elevar un número al exponente que deseemos (también puede ser una tecla xy), y al darle a "SHIFT" o "INV" podemos hacer la raíz del índice que queramos. Como ejemplo calcularemos la raíz de índice 5 de 24:
Tecleamos "SHIFT"; tecleamos ; tecleamos "5"; y por último, tecleamos "24"; la solución es: 1,888175023. Hay calculadoras que también incluyen la tecla
, que nos da el cubo de un número y su función inversa, esto es, al teclear "SHIFT" podemos utilizar la raíz cúbica.
Por último, otras calculadoras tienen la tecla que nos sirve, tras teclear "SHIFT", para lo mismo que la tecla vista dos líneas más arriba. Por tanto, para calcular raíces tendrás que utilizar las teclas
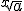 ó
ó 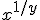 donde y sería el índice de la raíz.
donde y sería el índice de la raíz.
Caso de estudio
Resuelve con la calculadora:
a.1) 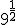 ; a.2)
; a.2) 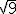
b.1) 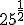 ; b.2)
; b.2) 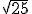
c.1) 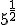 ; c.2)
; c.2) 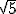
d.1) 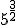 ; d.2)
; d.2) 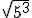
Puedes intuir de qué estamos hablando. Concrétalo en un expresión, y pincha en "Mostrar retroalimentación".
Veamos si sigue ocurriendo cuando el índice no es 2. Calcula ahora:
a.1) 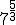 ; a.2)
; a.2) 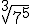 ;
;
b.1) 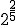 ; b.2)
; b.2) 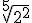
sigues obteniendo los mismos resultados ¿verdad?, de manera que intenta concluir con la generalización en letras de la potencia de un número fraccionario, y pincha después en Ver solución.
Importante
Las potencias de exponente fraccionario heredan las mismas propiedades que las vistas en los apartados anteriores. Además añaden la que acabamos de deducir:
| Potencia de exponente fraccionario | 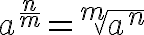 |
Pregunta de Elección Múltiple
Solución
Solución
Solución
Solución
Solución
Solución
Ejemplo o ejercicio resuelto
Ejercicios de repaso de las potencias:
- Pasa a raíz las siguientes potencias de exponente fraccionario:
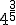
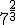
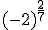
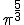
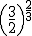
- Pasa a potencia de exponente fraccionario las siguientes raíces:
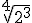
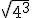
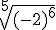
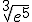
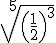
- Expresa estas potencias como potencia única, siempre con exponente positivo:
-

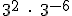
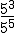
- Expresa en forma de potencia única las siguientes potencias, y calcula el resultado: