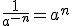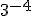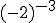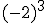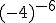4.2. Potencias de exponente entero
En el punto anterior hemos visto las potencias de exponente natural. En este vamos a dar un paso más, aumentando el campo de los exponentes a los números enteros. Evidentemente, el paso que tenemos que hacer es el del exponente negativo, puesto que los enteros son los números enteros positivos (los naturales) y los enteros negativos. Para comprender mejor como se hace la potencia de un número entero negativo, vamos a hacer algunos ejercicios de potencia.
Caso de estudio
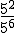
Calcula, utilizando esta vez, la definición de potencia, la misma potencia: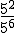
Cuando hayas contestado a las dos, pincha en "Mostrar retroalimentación".
Seguro que ahora eres capaz de enunciar la última igualdad con letras, de la misma manera que lo hicimos en el punto anterior.
Para comprobarlo haz clic en el botón.
Ejercicio resuelto
Del mismo modo podemos resolver la siguiente operación con potencias:
Calcula, utilizando las propiedades del apartado anterior, la siguiente potencia: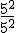 
Calcula, utilizando esta vez, la definición de potencia, la misma potencia: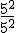
Importante
Propiedades de las potencias de exponente entero
Las potencias de exponente entero verifican las mismas propiedades que las potencias de exponente natural. Además de éstas, también verifican la propiedad vista más arriba, que resumimos en la siguiente tabla, en la que aparece también la importante propiedad de una potencia con exponente cero:
|
Potencia con exponente cero |
 |
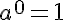Potencia de exponente negativo |
 |
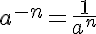Otra propiedad de las potencias, aunque puede parecer obvia, hay que tenerla clara y es que:
a1 = a
Ejemplo o ejercicio resuelto
Objetivos
La intención de esta propiedad es quitar las potencias que tengan un exponente negativo, no se trata de tener las potencias en el numerador o denominador, sino de quitar ese número negativo del exponente.
Hemos visto que cuando la potencia de exponente negativo está en el numerador, pasa al denominador con exponente positivo; nos preguntamos ahora, ¿qué pasará cuando la potencia de exponente negativo está en el denominador? Veámoslo.
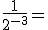{utilizando la propiedad de potencia de un número negativo} 
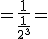{poniendo el 1 del numerador como fracción} 
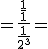{haciendo la división del doble cociente, o sea, "multiplicando en cruz"}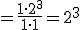 
Podemos concluir que: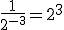 
; o en general: 