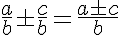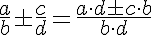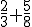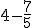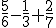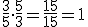3.2. Operaciones con fracciones
Importante
- por numerador, la suma o resta de los numeradores.
- por denominador, el común a ambas fracciones.
Si no tienen igual denominador, también puede optarse por la siguiente fórmula, que implícitamente las transforma en fracciones equivalentes como has visto en el punto 3.1:
Ejemplo o ejercicio resuelto
Importante
El producto de dos fracciones es otra fracción que tiene por numerador el producto de los numeradores y por denominador el producto de los denominadores:
El cociente o división de dos fracciones es otra fracción que tiene por numerador el producto de los extremos, y por denominador el producto de los medios:
ó equivalentemente
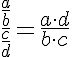
Con los siguientes vídeos puedes practicar las operaciones combinadas con números racionales. Recuerda la prioridad de las operaciones, que por supuesto siguen siendo válidas con las fracciones (primero los corchetes y paréntesis, luego las multiplicaciones y divisiones, y por último las sumas y restas, siempre de izquierda a derecha).
En el conjunto de los números racionales se verifican las siguientes propiedades:
Sean a, b y c números reales cualesquiera se cumplen las siguientes propiedades.
|
Propiedades de la suma
|
Propiedades de la multiplicación
|
|
Conmutativa
a + b = b + a
|
Conmutativa
a · b = b · a
|
|
Asociativa
(a+b)+c = a+(b+c)
|
Asociativa
(a · b) · c = a · (b · c)
|
|
Existencia de elemento neutro
a+0 = a
0 es el elemento neutro de la suma
|
Existencia de elemento neutro
a · 1 = a
1 es el elemento neutro de la multiplicación
|
|
Existencia de elemento simétrico
a+(-a) = 0
-a es el inverso o simétrico de a respecto de la multiplicación.
|
Existencia de elemento simétrico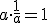
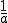 es el inverso o simétrico de a respecto de la multiplicación.
|
|
Propiedad distributiva de la suma respecto a la multiplicación (a + b) · c = a · c + b · c |
|
Fíjate que la nueva propiedad que añaden los números racionales, respecto a los números enteros, es la existencia de elemento simétrico para la multiplicación. Es decir, dada una fracción, siempre podemos encontrar otra de forma que al multiplicarlas se obtenga el valor 1. Por ejemplo, la fracción simétrica de 3/5 es 5/3 ya que:
En definitiva, el simétrico de la fracción a/b, es la fracción b/a.
Objetivos
En el siguiente enlace a una página editada por el Gobierno de Canarias, tienes una amplia gama de actividades dedicadas a las operaciones con fracciones.
Ejemplo o ejercicio resuelto
En una mesa, mientras se toma su bocadillo, Meki, una chica del instituto, llama a su profe: "Esto debe estar mal, me salen tres cuartos y no se puede dividir". Paqui, que es profe de francés pero suele hacer la compra de su casa, salta: "Pues claro que se puede, ayer compré tres cuartos de kilo de carne y me pusieron 750 gramos". Suena el timbre y todos a clase.
- El profesor sabe que en su próxima clase encontrará más chicas que chicos.
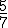del grupo son chicas y en total son 28. ¿Cuántas chicas hay en esa clase?
- Paqui debe ir al cajero a sacar dinero. Piensa que si gasta
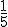de su dinero en la entrada para un coche, 
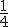en comprarse los muebles que necesita, la décima parte de sus ahorros en un ordenador y 
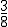de los mismos en liquidar lo que le falta para terminar de pagar su casa,
aún le quedarán 375 €. "No está nada mal", piensa ella. Por cierto,
¿cuánto dinero tiene Paqui?
- Por su parte, Meki que tiene 250 € ahorrados, piensa gastarse
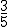de su dinero en ropa, 
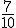de lo que aún le quede en música y 30 € en un libro. Lo que le sobre se lo
regalará a su hermana. ¿Es muy generosa con su hermana?
- El profesor de matemáticas debe corregir los exámenes de una clase. Ayer corrigió
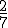de todos los exámenes, hoy piensa corregir 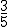de los que le quedan, y así para mañana sólo le restarán 8. ¿Cuántos alumnos/as se presentaron al examen?
