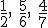3.1. Fracciones equivalentes
El ciclo de la Luna dura aproximadamente 30 días. Cada día, una pequeña parte del ciclo se va cumpliendo, pero también podemos decir que un pequeño porcentaje del ciclo se va completando.
La siguiente imagen animada representa la zona visible de la Luna según el porcentaje de ciclo transcurrido, de tal manera que recorre todas las fases intermedias (luna nueva, creciente, luna llena y menguante).
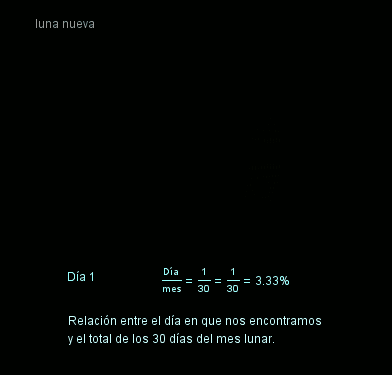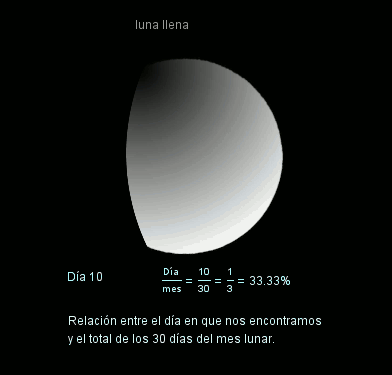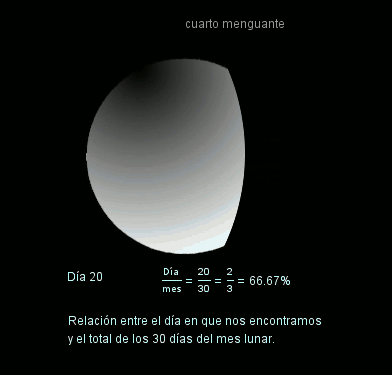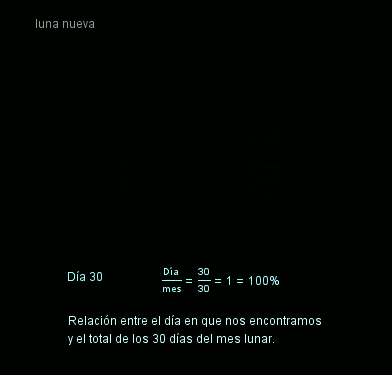
Si te fijas atentamente en la imagen animada anterior, puedes ver que en ocasiones aparecen dos fracciones igualadas pero que no tienen el mismo numerador ni denominador, son las llamadas fracciones equivalentes. Junto a ellas aparece un mismo porcentaje asociado a ambas, ya que tanto una como otra representan al mismo número racional.
Por ejemplo, si haces la división (prueba con la calculadora) puedes comprobar que las siguientes fracciones dan el mismo resultado:
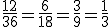
Fíjate que el numerador y el denominador se han dividido sucesivamente por el mismo factor, el dos, salvo en el último paso que se han dividido por tres. Por tanto, si en una fracción multiplicas o divides el numerador y denominador por el mismo número, estarás obteniendo el mismo resultado, determinan un mismo número racional y se dicen que son fracciones equivalentes.
Actividad
Para comprobar si dos fracciones son equivalentes, se multiplican sus términos en cruz; cuando el producto de extremos es igual al producto de los medios, las fracciones son equivalentes y por tanto definen el mismo número racional.
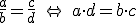
O lo que es lo mismo, si en una fracción se multiplica o se divide el numerador y el denominador por un mismo número distinto de cero, se obtiene una fracción equivalente a la original:
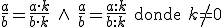
Simplificar una fracción es dividir el numerador y el denominador por un mismo número, de forma que se obtiene una fracción equivalente con números más pequeños. Una fracción es irreducible (no admite simplificación) cuando el numerador y el denominador son primos entre sí. Por ejempl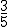o 
o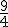 
son fracciones irreducibles.
Las fracciones en las que el numerador es un número menor que el denominador, se denominan fracciones propias.
Las fracciones equivalentes serán el concepto en el que nos basaremos para poder comparar, sumar y restar fracciones, ya que podremos buscar siempre fracciones equivalentes a las dadas que entre ellas tengan el mismo denominador y no nos pase como uno de los personajes de la película Granujas de medio pelo dirigida por Woody Allen, de la que a continuación se muestra un clip, que se lía un poco al sumar y comparar fracciones.
En efecto, para poder comparar dos fracciones y poder saber cuál es mayor o menor, conviene pasarlas a fracciones equivalentes que tengan el mismo denominador, de forma que será mayor o menor la que tenga mayor o menor numerador respectivamente.
Por ejemplo, sin utilizar la calculadora, nos planteamos qué fracción es mayor, si 2/5 o 3/7. Para pasarlas a común denominador, dicho denominador tendrá que ser un múltiplo de 5 y de 7. Se puede optar por calcular el mínimo común múltiplo de los denominadores, o bien vale multiplicarlos directamente, luego un denominador común sería el 35. La primera fracción habría que multiplicarla por siete y pasaría a ser 14/35; mientras que la segunda fracción habría que multiplicarla por 5 y pasaría a ser 15/35. Por tanto la segunda fracción es un poco mayor, y deducimos que 3/7 > 2/5.
Importante
Para reducir dos o más fracciones a común denominador basta multiplicar el numerador y el denominador de cada fracción por el número que resulta de dividir el mínimo común múltiplo de los denominadores entre cada denominador.
Otra forma.
Para reducir dos o más fracciones a común denominador basta
multiplicar el numerador y el denominador por el producto de los denominadores de las otras fracciones.
De dos fracciones que tienen el mismo denominador, es mayor la que tiene mayor numerador.
Ejemplo o ejercicio resuelto
